In order to apply Bayes' rule to updating the beliefs, there have to be some prior beliefs to start with. These prior beliefs are needed for the variables which are at the beginning of the causal chains of the model. In principle the prior probabilities should summarise all the information there is available. In practice the choice of the model structure is often practical and does not reflect the exact beliefs of the modeller and the same holds true for prior probabilities.
When considering the prior probability for a variable, the first question to ask is whether the variable is really at the beginning of the causal chain. Often there are sets of variables for which there is reason to believe that their values are dependent. This belief is easier to express in terms of model structure than in terms of prior probability. One can postulate a hidden variable which determines the probabilities for the set of dependent variables. The problem of determining a prior is simplified because instead of assigning a separate prior for all variables in the set, only one prior is needed for the hidden variable. The process can be iterated and in the end one is usually left with only a few variables which need a prior.
Once all the structural prior knowledge is used, there is typically not very much information about the variables at the beginning of causal chains. It is then instructive to consider so called uninformative priors. The name refers to a principle according to which all models should be ``given an equal chance'' if there is no information to choose between them. The principle has theoretical justification only in cases where symmetries of the problem suggest that the models have the same prior probability. In other cases, the method can be seen as a practical choice which guarantees that the hypothesis space is used efficiently and the learning system is initially prepared to believe in any of the models it can represent.
For real valued parameters, it is usually not a good idea to simply choose a uniform prior for the parameters. The problem again is that probability density has no importance per se. A nonlinear transformation of the parameter alters the density differently for different values of the parameter. This means that a uniform density is not uniform after the parameter transformation although the reparameterisation does not alter the model in any way, and shows that it is not possible to assess the uninformative prior for a parameter without knowing what is the role of the parameter in the model.
It is instructive to consider how much the probability distribution
which the model gives to the observations changes when the parameters
of the model change. Let us take for example the Gaussian
distribution parameterised by the mean ![]() and standard deviation
and standard deviation
![]() . For this parameterisation, the relative effect of change in
. For this parameterisation, the relative effect of change in
![]() depends on the variance
depends on the variance ![]() : if
: if ![]() is large, then the
change in
is large, then the
change in ![]() has to be large before the probability assignments for
observations change significantly. If
has to be large before the probability assignments for
observations change significantly. If ![]() is small, then a small
change in
is small, then a small
change in ![]() causes a relatively large change in the probability
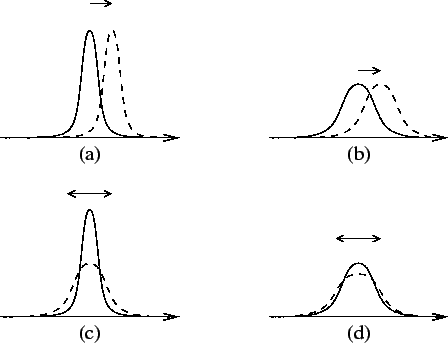
assignments. This is depicted in figures 4a and
4b. Similarly, figures 4c and
4d illustrate how the relative effect of change in
variance depends on the variance.
causes a relatively large change in the probability
assignments. This is depicted in figures 4a and
4b. Similarly, figures 4c and
4d illustrate how the relative effect of change in
variance depends on the variance.
 |
The size of change in the observation probabilities caused by the
change of parameters can be measured by the Fisher information matrix
![]() whose elements
whose elements
![]() can be
defined as
can be
defined as
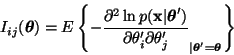 |
(24) |
A uniform density in the information geometry space corresponds to a
density which is proportional to
![]() .
This is the uninformative Jeffreys' prior. For the
Gaussian density, for instance, this corresponds to a density
.
This is the uninformative Jeffreys' prior. For the
Gaussian density, for instance, this corresponds to a density
![]() . This does not produce a proper density
because the normalising factor would be infinite. The uninformative
prior can nevertheless guide the choice of the prior. For instance, a
small adjustment taking into account a finite range for
. This does not produce a proper density
because the normalising factor would be infinite. The uninformative
prior can nevertheless guide the choice of the prior. For instance, a
small adjustment taking into account a finite range for ![]() and
and
![]() will result in a prior which can be normalised.
will result in a prior which can be normalised.
The Fisher information matrix
![]() is also
important because the posterior densities tend to be approximately
Gaussian and have a covariance proportional to
is also
important because the posterior densities tend to be approximately
Gaussian and have a covariance proportional to
![]() , where N is the number of samples.
This property can be utilised for modifying the MAP estimator by
multiplying the posterior density by the volume
, where N is the number of samples.
This property can be utilised for modifying the MAP estimator by
multiplying the posterior density by the volume
![]() . This results in an approximation
of posterior probability mass whose maximisation has a more solid
theoretical justification than the maximisation of density. It is
noteworthy that in models lacking hyperparameters, a combination of
Jeffreys' prior and the modified MAP estimate is equal to ML
estimation.
. This results in an approximation
of posterior probability mass whose maximisation has a more solid
theoretical justification than the maximisation of density. It is
noteworthy that in models lacking hyperparameters, a combination of
Jeffreys' prior and the modified MAP estimate is equal to ML
estimation.
In the information geometry space, the parameters tend to have spherically symmetric Gaussian posterior densities and their skewness tends to be smaller than in other parameterisations. This property is useful for parametric approximation of posterior densities because a Gaussian approximation, which is often mathematically convenient, is more valid. The spherical symmetry, on the other hand, can be utilised in gradient descent algorithms because it means that the gradient points to the minimum. The gradient computed in information geometry space is known as the natural gradient and it has been applied to learning neural networks [2].