Supervised vs. unsupervised learning

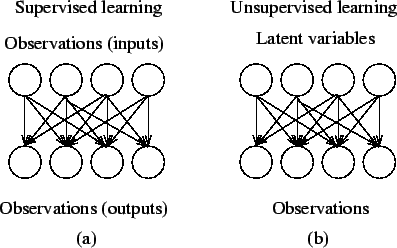
From a theoretical point of view, supervised and unsupervised learning differ only in the causal structure of the model. In supervised learning, the model defines the effect one set of observations, called inputs, has on another set of observations, called outputs. In other words, the inputs are assumed to be at the beginning and outputs at the end of the causal chain. The models can include mediating variables between the inputs and outputs.

In unsupervised learning, all the observations are assumed to be caused by latent variables, that is, the observations are assumed to be at the end of the causal chain. In practice, models for supervised learning often leave the probability for inputs undefined. This model is not needed as long as the inputs are available, but if some of the input values are missing, it is not possible to infer anything about the outputs. If the inputs are also modelled, then missing inputs cause no problem since they can be considered latent variables as in unsupervised learning.

  

Figure 2: The causal structure of (a) supervised and (b) unsupervised learning. In supervised learning, one set of observations, called inputs, is assumed to be the cause of another set of observations, called outputs, while in unsupervised learning all observations are assumed to be caused by a set of latent variables.

Figure 2 illustrates the difference in the causal structure of supervised and unsupervised learning. It is also possible to have a mixture of the two, where both input observations and latent variables are assumed to have caused the output observations.

With unsupervised learning it is possible to learn larger and more complex models than with supervised learning. This is because in supervised learning one is trying to find the connection between two sets of observations. The difficulty of the learning task increases exponentially in the number of steps between the two sets and that is why supervised learning cannot, in practice, learn models with deep hierarchies.

In unsupervised learning, the learning can proceed hierarchically from the observations into ever more abstract levels of representation. Each additional hierarchy needs to learn only one step and therefore the learning time increases (approximately) linearly in the number of levels in the model hierarchy.

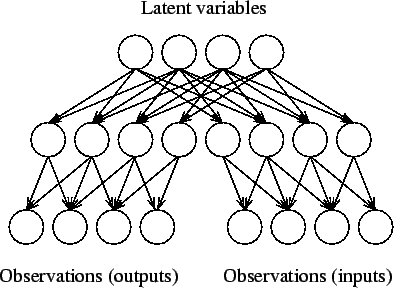
If the causal relation between the input and output observations is complex -- in a sense there is a large causal gap -- it is often easier to bridge the gap using unsupervised learning instead of supervised learning. This is depicted in figure 3. Instead of finding the causal pathway from inputs to outputs, one starts building the model upwards from both sets of observations in the hope that in higher levels of abstraction the gap is easier to bridge. Notice also that the input and output observations are in symmetrical positions in the model.

  

Figure 3: Unsupervised learning can be used for bridging the causal gap between input and output observations. The latent variables in the higher levels of abstraction are the causes for both sets of observations and mediate the dependence between inputs and outputs.