Converted feedforward equations

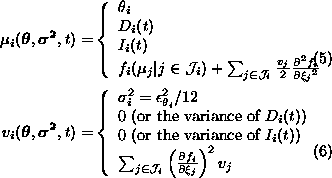
We shall now collect together the results derived in this section.
  $$\begin{align} \mu_i(\boldsymbol{\theta}, \boldsymbol{\sigma^2}, t) = & \left\{... ...rac{\partial f_i}{\partial \xi_j} \right)^2 v_j \end{array} \right.\end{align}$$

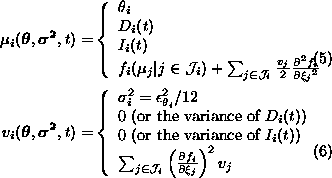
Substituting $\epsilon_{\theta_i} = (12 v_i)^{1/2}$ into equation 7 yields equation 15 for the expected description length L_E.  

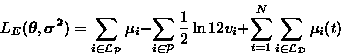$$L_E(\boldsymbol{\theta}, \boldsymbol{\sigma^2}) = \sum_{i \... ... \ln 12 v_i + \sum_{t=1}^N \sum_{i \in \mathcal{L_D}} \mu_i(t)$$ (9)

Equations 13 and 14 describe how to convert a standard feedforward network into a network where the output of each neuron is assigned a mean and a variance. Equation 15 then defines the MDL-based cost function for such a network. The gradient of the cost function can be computed using standard backpropagation algorithm.