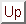

Next: Expectation of a function
Up: Computing the expectation of
Previous: Feedforward equations
Let us define 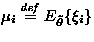 . Taking
expectation over
. Taking
expectation over 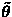 from equation 4
yields
from equation 4
yields
| 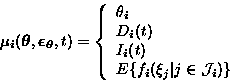 |
(6) |
and expectation from equation 5 yields
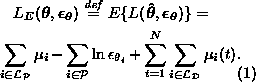
We have dropped the subscripts from the expectation operators, but
they are always taken over 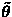 .
.
Harri Lappalainen
5/19/1998
![]() . Taking
expectation over
. Taking
expectation over ![]() from equation 4
yields
from equation 4
yields