We still need the variances vj. Since each error ![]() is evenly distributed in the range
is evenly distributed in the range ![]() , the variances of the parameters are given by
, the variances of the parameters are given by
![]() . The variance of the inputs and
desired outputs can be assumed to be zero, or they can be assigned
some values if there is prior knowledge about, for example, the
equipment used to measure the values.
. The variance of the inputs and
desired outputs can be assumed to be zero, or they can be assigned
some values if there is prior knowledge about, for example, the
equipment used to measure the values.
In order to compute the variance of the function fi, we shall approximate it with first order Taylor's series expansion.
| |
(7) |
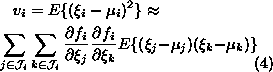
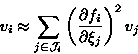 |
(8) |