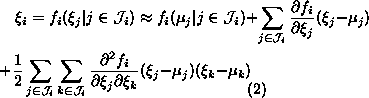
Taking expectation from both sides of equation 8 yields
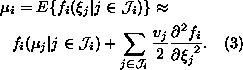
Here we have denoted the variance of
Equations 6 and 7 show that we could compute the expected description length if we knew how to evaluate the expectations of the functions fi.
Let ![]() be a function whose expectation
value we would like to compute. As before, we shall approximate fi
with its second order Taylor's series expansion. However, we are not
going to expand fi with respect to the discretised parameters
be a function whose expectation
value we would like to compute. As before, we shall approximate fi
with its second order Taylor's series expansion. However, we are not
going to expand fi with respect to the discretised parameters
![]() of the network but the direct parameters
of the network but the direct parameters ![]() of the
function fi. The expansion is thus computed about the expectation
values
of the
function fi. The expansion is thus computed about the expectation
values ![]() .
.
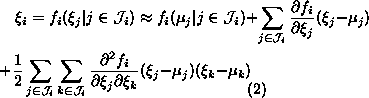
Taking expectation from both sides of equation 8 yields
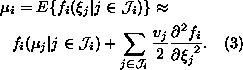
Here we have denoted the variance of ![]() by vj:
by vj: ![]() . The first order terms disappear because
. The first order terms disappear because
![]() . We have also assumed that for all
. We have also assumed that for all ![]() , either
, either ![]() and
and ![]() are uncorrelated or
are uncorrelated or
![]() , which removes the second order
cross terms.
, which removes the second order
cross terms.