Let ![]() . The expectation
to be approximated is then
. The expectation
to be approximated is then
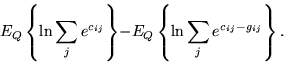
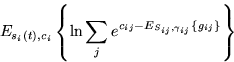
The expectation ![]() is similar to
equation 1 and equals to
is similar to
equation 1 and equals to
![]()
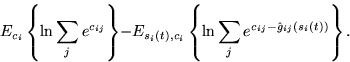
Next, let us concider a second order Taylor's series expansion about
![]() and
and ![]() . Notice that the first order terms and
all second order crossterms disappear in the expectations and only the
constant and the pure second order terms remain. This is because the
variables are independent in the ensemble.
. Notice that the first order terms and
all second order crossterms disappear in the expectations and only the
constant and the pure second order terms remain. This is because the
variables are independent in the ensemble.
| |
(2) |
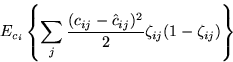
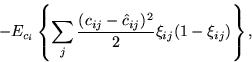
![]()
![]()
| |
(3) |
![]()
![]()
![]()
![]()
| |
(4) |
Some care has to be taken with the approximation resulting from the
Taylor's series expansion because it utilises only local information
about the shape of the posterior pdf. For instance, if the mean
![]() happens to be in a valley between two Gaussians, the
term in equation 4 will be negative. It then looks like the
Kullback-Leibler information can be decreased by increasing
happens to be in a valley between two Gaussians, the
term in equation 4 will be negative. It then looks like the
Kullback-Leibler information can be decreased by increasing
![]() . This only holds for small
. This only holds for small ![]() , however. At
some point after the distribution of si(t) has become broader than
the separation between the two Gaussians, the Kullback-Leibler
information starts to increase as
, however. At
some point after the distribution of si(t) has become broader than
the separation between the two Gaussians, the Kullback-Leibler
information starts to increase as ![]() increases.
increases.
In order to avoid the problem, only positive terms of equations 3 and 4 will be included. The final approximation is thus equation 2 plus the positive terms of equations 3 and 4.