

Next: Simulations
Up: Ensemble Learning for Independent
Previous: Model for the measurements
Given the measurements, the unknown variables of the model are the
source signals, the mixing matrix, the parameters of the noise and
source distributions and the hyperparameters. The posterior P is
thus a pdf of all these unknown variables. For notational simplicity,
we shall sometimes denote these n variables by 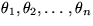 .
.
In order to make the approximation of the posterior pdf
computationally tractable, we shall choose the ensemble Q to be a
Gaussian pdf with diagonal covariance. The ensemble has twice as many
parameters as there are unknown variables in the model because each
dimension of the posterior pdf is parametrised by a mean and variance
in the ensemble. A hat over a symbol denotes the mean and
a tilde the variance of the corresponding variable.
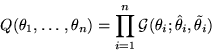
The factorised ensemble makes the computation of the Kullback-Leibler
information 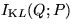 simple since the logarithm can be split into a
sum of terms: the terms
simple since the logarithm can be split into a
sum of terms: the terms 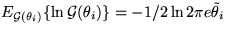 (entropies of Gaussian distributions) and terms
(entropies of Gaussian distributions) and terms
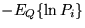 , where Pi are the factors of the posterior pdf.
Notice that the posterior pdf factorises into simple terms due to the
hierarchical structure of the model; the posterior pdf equals to
the joint pdf divided by a normalising term.
, where Pi are the factors of the posterior pdf.
Notice that the posterior pdf factorises into simple terms due to the
hierarchical structure of the model; the posterior pdf equals to
the joint pdf divided by a normalising term.
To see how to compute the terms 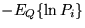 , let
, let 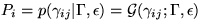 .
.
| 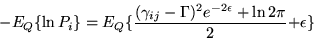 |
(1) |
It is easy to show that this equals to
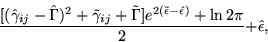
since according to the choice of Q, the parameters 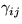 ,
,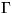 and
and 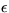 have independent Gaussian distributions.
have independent Gaussian distributions.
The most difficult terms are the expectations of 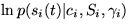 . Approximation for the expectation of this form is
given in appendix A.
. Approximation for the expectation of this form is
given in appendix A.
The normalising term in the posterior pdf only depends on those
variables which are given, in this case 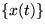 , and can therefore
be neglected when minimising the Kullback-Leibler information
, and can therefore
be neglected when minimising the Kullback-Leibler information 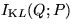 .
.


Next: Simulations
Up: Ensemble Learning for Independent
Previous: Model for the measurements
Harri Lappalainen
7/10/1998
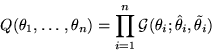
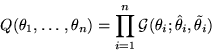
![]() , let
, let ![]() .
.
![]()
![]() . Approximation for the expectation of this form is
given in appendix A.
. Approximation for the expectation of this form is
given in appendix A.
![]() , and can therefore
be neglected when minimising the Kullback-Leibler information
, and can therefore
be neglected when minimising the Kullback-Leibler information ![]() .
.