It was mentioned earlier that the efficiency of the algorithm is based
on finding a (small) set of winners, that is, neurons for which the
winning strength is not zero, and then calculating the winning
strengths for that set only. The set of winners should include those
neurons i for which 
for all j.
In order to find the set of winners we go through all the neurons and
at each step update the set. Suppose we have gone through the neurons
from 1 to i-1 and for those neurons the set of winners is
. Then we start looking at neuron i and update the
set of winners to 
. If 
, then 
is
always zero. We don't accept the neuron i to the set, leaving the
set intact, that is, 
. If 
, we
start comparing the neuron i pairwise with the neurons 
. In each comparison we compute the winning ratios
and 
according to equation 3.6. If
we shall discard neuron i and move to the next neuron
i+1. If 
, we shall remove the neuron j from the set
. If for all we shall
add the neuron i to the set . Figure 3.4
gives a geometric interpretation for the comparison between two
neurons.
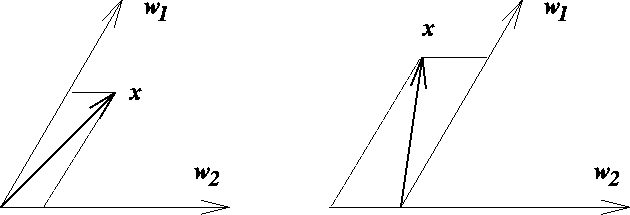
Figure 3.4:
At the left, the input is ``between'' the weight vectors and
projection for both neurons is positive. Both neurons are
accepted in comparison. At the right, only the projection to
neuron 1 is positive. From the point of view of neuron 2, the
input is ``behind'' the neuron 1. Neuron 1 is accepted and neuron
2 discarded in comparison.
The efficiency of this process is due to the fact that at each step a new neuron is compared only with the neurons currently present in the set of winners. A new neuron is not compared with those neurons that have already been discarded from the set of winners. This can, on the other hand, make the resulting set of winners vary with different orders of neurons. This is exemplified in figure 3.5. Whether neuron 3 will be chosen to the set of winners depends on the order of the neurons. In practice, neurons which could have been left out from the set, if the order of neurons had been different, will anyway have a very small winning strength, and thus the final outputs vary only slightly. If the possible variations in the set of winners turn out to be a problem, it is possible to go through the neurons again, and to check whether any neurons in the set of winners should be discarded. This way the neuron 3 in our example would always be discarded.
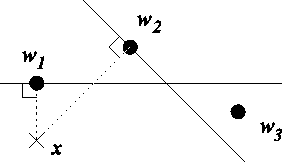
Figure 3.5:
An example of a situation where the set of winners varies
according to the order of neurons. All vectors are supposed to
be nearly parallel and 3-dimensional. The figure shows a view
from top (cf. a map of a small area on globe). Neuron 3 is
discarded in comparison with neuron 2 and accepted in comparison
with neurons 1. Neuron 1 will always be accepted to the set of
winners and neuron 2 will always be discarded. Whether neuron 3
is accepted into the set of winners depends on the order of the
neurons. If the order is 2, 3 and 1, neuron 3 will be discarded
in comparison with neuron 2. If the order is 1, 2 and 3, neuron 2
will be discarded in comparison with neuron 1, and neuron 3 will
be accepted in comparison with neuron 1.