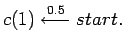 |
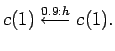 |
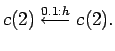 |
|
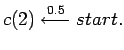 |
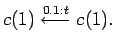 |
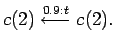 |
Let us consider the following simple HMM written as a LOHMM:
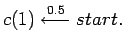 |
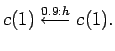 |
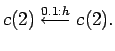 |
|
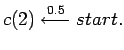 |
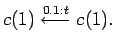 |
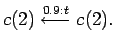 |
Given sequences ![]() and
and ![]() as data, the structure
shown above and a uniform prior over parameters, we now ask, what
would the different estimators give as parameters. In fact, all of
them would give 0.5 for the selection between the coins, but the
probabilities
as data, the structure
shown above and a uniform prior over parameters, we now ask, what
would the different estimators give as parameters. In fact, all of
them would give 0.5 for the selection between the coins, but the
probabilities ![]() and
and ![]() for the coins
for the coins ![]() and
and ![]() to produce
heads are of more interest.
to produce
heads are of more interest.
There are three fixed points for the maximum a posteriori (or maximum
likelihood) estimator (Eq. 3). The first one is a saddle
point at ![]() ,
, ![]() and the two others are the global maxima
and the two others are the global maxima
![]() ,
, ![]() and
and ![]() ,
, ![]() . Using random
initialisation, the Baum-Welch algorithm would end up in the latter
two with equal probabilities and to the first one with probability
0. This estimator would conclude from the data that one of the coins
produces heads every time and the other only tails. If the estimated
model is tested with a sequence
. Using random
initialisation, the Baum-Welch algorithm would end up in the latter
two with equal probabilities and to the first one with probability
0. This estimator would conclude from the data that one of the coins
produces heads every time and the other only tails. If the estimated
model is tested with a sequence ![]() , it would give a
likelihood of exactly 0. From this failure one could conclude, that
maximum likelihood estimator does not prepare well for new data if
there is a limited amount of data available for learning.
, it would give a
likelihood of exactly 0. From this failure one could conclude, that
maximum likelihood estimator does not prepare well for new data if
there is a limited amount of data available for learning.
The Bayes estimator (Eq. 4) is hard to
evaluate in general, but in this case one can use symmetry to conclude
that it is ![]() ,
, ![]() . Since the estimator is always unique,
it cannot decide which coin produces more heads (resp. tails).
. Since the estimator is always unique,
it cannot decide which coin produces more heads (resp. tails).
The componentwise Bayes estimator
(Eq. 5) has also three fixed points. The
first one is the saddle point at ![]() ,
, ![]() in analogy with
the map-estimator. The stable points are now at
in analogy with
the map-estimator. The stable points are now at ![]() ,
,
![]() and
and ![]() ,
, ![]() . Again, random
initialisation will decide which one is chosen. The cB estimator
seems to combine the good properties of the other two. It can operate
with limited amount of data like the Bayes estimator, but can avoid
the symmetrical solution.
. Again, random
initialisation will decide which one is chosen. The cB estimator
seems to combine the good properties of the other two. It can operate
with limited amount of data like the Bayes estimator, but can avoid
the symmetrical solution.