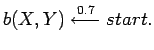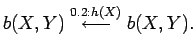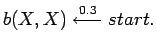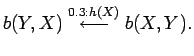LOGICAL HIDDEN MARKOV MODELS

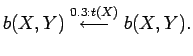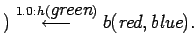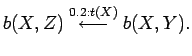This section gives a short introduction to logical hidden Markov models. A more thorough introduction can be found in [9].

A logical hidden Markov model (LOHMM) is a generative model, which can be described as a set of transitions and a set of selection probabilities for variables. For example

$$b(X,Y) \stackrel{0.7}{\longleftarrow} start. b(X,Y) \stackrel{0.2:h(X)}{\longleftarrow} b(X,Y).$$

$$b(X,X) \stackrel{0.3}{\longleftarrow} start. b(Y,X) \stackrel{0.3:h(X)}{\longleftarrow} b(X,Y).$$ (1)

$$b(X,Y) \stackrel{0.3:t(X)}{\longleftarrow} b(X,Y).$$

$$b(X, ) \stackrel{1.0:h(\mbox{\it green})}{\longleftarrow} b(\mbox{\it red},\mbox{\it blue}). b(X,Z) \stackrel{0.2:t(X)}{\longleftarrow} b(X,Y).$$

could be interpreted as follows: The hidden state $b$ has two arguments, the colours of the left and right ball. In the beginning, it is more probable to have same colours than by selecting independently. At each time step, a coin is thrown. The observation contains the result of the coin throw ($h$ or $t$) and the colour of the left ball. If we observe a heads, it is possible that the balls are switched. If we observe a tail, the right ball might be replaced by a new one. There is one exception: if the left ball is red and the right one is blue, the observation is a heads with green, and the left ball is replaced.

Each transition includes 1) the logical atom called body which is the source of the transition; 2) the logical atom called head which is the destination of the transition; 3) the logical atom which is observed¹ and 4) the probability associated to the transition. The names body and head and the direction to the left are used since transitions of a LOHMM can be seen as augmented logical clauses.

For reasons that will become clear, we need the more specific relation among atoms. An atom $a$ is (strictly) more specific than atom $b$ if $b$ can be transformed into $a$ by substituting some of its variables, but $a$ cannot be transformed into $b$ similarly. For example $a(X,X)$ is more specific than $a(Y,Z)$ since the variables $Y$ and $Z$ can be substituted with $X$, but $X$ cannot be substituted with both $Y$ and $Z$ at the same time.

A logical sequence can be generated from a LOHMM by repeating the steps below. At each time point, the process is in a (hidden) state represented by a logical atom. It starts in the special state called start.

1. The body, which is most specific for the current state, is selected (deterministically).
2. A transition is selected according to the transition probabilities.
3. Variables that appear in the body are instantiated to match the current state.
4. Other variables are instantiated using a selection probability $\mu$.
5. The (instantiated) observation is added to the logical sequence.
6. The (instantiated) head is used as the current state and the LOHMM is left unchanged.

We use a simple selection distribution $\mu$ here: Each argument of an atom has a type and each type has a distribution over constants associated to it. In our example, the only type $colour$ is defined as $\{0.4:$red$, 0.3:$green$, 0.3:$blue$\}$.

A LOHMM is well-defined, if there is a unique most specific body for every state and if the transition probabilities for a single body sum up to one. For example, if there were bodies $b(X,X)$ and $b(X,$red$)$ in a LOHMM and the current state was $b($red$,$red$)$, one could not say which body to use. The problem is avoided by adding transitions with the body $b($red$,$red$)$.

LOHMMs combine logical reasoning with probabilistic (statistical) modelling. For example, if we know the LOHMM produced the sequence $h($green$),h($blue$)$, we can compute that the probability of being in the hidden state $b($green$,$blue$)$ at time $1$ is $0.43$. If we also know, that the third observation is $h($green$)$, we can be certain that the hidden state at time $1$ was in fact $b($green$,$blue$)$.