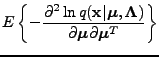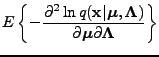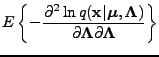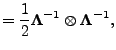Next: OPTIMIZATION ALGORITHMS ON RIEMANNIAN
Up: INFORMATION GEOMETRY AND NATURAL
Previous: COMPUTING THE RIEMANNIAN METRIC
For the univariate Gaussian distribution parameterized by mean and variance
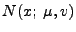 , we have
, we have
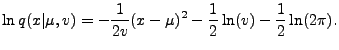 |
(7) |
Further,
The resulting Fisher information matrix is diagonal and its inverse is given
simply by
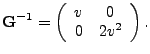 |
(11) |
In the case
of univariate Gaussian distribution, natural gradient has a rather
straightforward intuitive interpretation as seen in
Figure 1. Compared to conventional
gradient,
natural gradient compensates for the fact that changing the parameters of
a Gaussian with small variance has much more pronounced effects than
when the variance is large. The differences between the gradient
and the natural gradient are illustrated in Figure 2
with a simple example.
Figure:
The absolute change in the mean of the Gaussian in figures (a)
and (b) and the absolute change in the variance of the Gaussian in
figures (c) and (d) is the same.
However, the relative effect is much larger when the variance is small
as in figures (a) and (c) compared to the case when the variance is
high as in figures (b) and (d) (Valpola, 2000).
![\begin{figure}\centering
\subfigure[]{
\epsfig{file=meanchange_lowvar.eps,widt...
...ure[]{
\epsfig{file=varchange_highvar.eps,width=0.22\textwidth}}
\end{figure}](img33.png) |
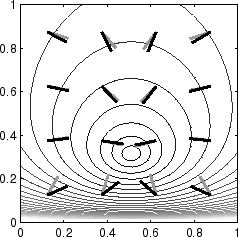
Figure:
The contours show an objective function of the mean (horizontal
axis) and the variance (vertical axis) of a Gaussian
model. Gradient (gray line) and natural gradient (black line) are
plotted at 16 different points.
 |
For the multivariate Gaussian distribution parameterized by mean and
precision
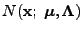 , we have
, we have
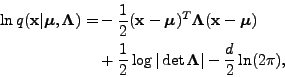 |
(12) |
where 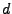 is the dimension of
is the dimension of
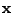 .
Rather straightforward differentiation yields
.
Rather straightforward differentiation yields
where 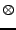 is the direct product, also known as the Kronecker product.
Because the cross term is zero, the resulting full Fisher information
matrix is block diagonal and can be inverted simply by
is the direct product, also known as the Kronecker product.
Because the cross term is zero, the resulting full Fisher information
matrix is block diagonal and can be inverted simply by
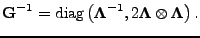 |
(16) |
This result for the precision may not be very useful in practice, as
the approximations used in most applications have a more restricted
form such as a Gaussian with a factor analysis covariance
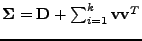 , where
, where
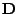 is a diagonal matrix, or a Gaussian Markov random field.
is a diagonal matrix, or a Gaussian Markov random field.



Next: OPTIMIZATION ALGORITHMS ON RIEMANNIAN
Up: INFORMATION GEOMETRY AND NATURAL
Previous: COMPUTING THE RIEMANNIAN METRIC
Tapani Raiko
2007-04-18
![]() , we have
, we have
![\begin{figure}\centering
\subfigure[]{
\epsfig{file=meanchange_lowvar.eps,widt...
...ure[]{
\epsfig{file=varchange_highvar.eps,width=0.22\textwidth}}
\end{figure}](img33.png)

![]() , we have
, we have