


Next: COMPUTING THE RIEMANNIAN METRIC
Up: Natural Conjugate Gradient in
Previous: INTRODUCTION
Let
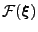 be a scalar function defined on the manifold
be a scalar function defined on the manifold
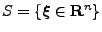 . If
. If 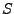 is a Euclidean space and
the coordinate system
is a Euclidean space and
the coordinate system
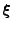 is orthonormal, the length of a
small incremental vector
is orthonormal, the length of a
small incremental vector
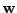 is given by
is given by
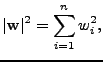 |
(1) |
where 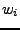 is the
is the 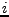 th component of the vector
th component of the vector
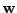 . The direction
of steepest ascent, i.e. the direction that maximizes
. The direction
of steepest ascent, i.e. the direction that maximizes
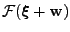 under the constraint
under the constraint
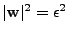 for a sufficiently
small constant
for a sufficiently
small constant 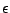 , is given by the gradient
, is given by the gradient
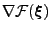 .
.
If the space 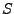 is a curved manifold, there is no orthonormal
coordinate system and the the length of a vector
is a curved manifold, there is no orthonormal
coordinate system and the the length of a vector
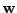 differs from
the value given by
Eq. (1). Riemannian manifolds are an important
class of curved manifolds, where the length is given by
the positive quadratic form
differs from
the value given by
Eq. (1). Riemannian manifolds are an important
class of curved manifolds, where the length is given by
the positive quadratic form
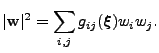 |
(2) |
The
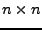 matrix
matrix
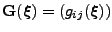 is called the
Riemannian metric tensor and it may depend on the point of origin
is called the
Riemannian metric tensor and it may depend on the point of origin
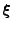 . On a Riemannian manifold, the direction of steepest ascent is
given by the natural gradient (Amari, 1998)
. On a Riemannian manifold, the direction of steepest ascent is
given by the natural gradient (Amari, 1998)
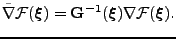 |
(3) |
For the space of probability distributions
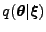 ,
the most common Riemannian metric tensor is
given by the Fisher information (Amari, 1985)
,
the most common Riemannian metric tensor is
given by the Fisher information (Amari, 1985)
where the last equality is valid given certain regularity
conditions (Murray and Rice, 1993).
Subsections



Next: COMPUTING THE RIEMANNIAN METRIC
Up: Natural Conjugate Gradient in
Previous: INTRODUCTION
Tapani Raiko
2007-04-18
![]() be a scalar function defined on the manifold
be a scalar function defined on the manifold
![]() . If
. If ![]() is a Euclidean space and
the coordinate system
is a Euclidean space and
the coordinate system
![]() is orthonormal, the length of a
small incremental vector
is orthonormal, the length of a
small incremental vector
![]() is given by
is given by
![]() is a curved manifold, there is no orthonormal
coordinate system and the the length of a vector
is a curved manifold, there is no orthonormal
coordinate system and the the length of a vector
![]() differs from
the value given by
Eq. (1). Riemannian manifolds are an important
class of curved manifolds, where the length is given by
the positive quadratic form
differs from
the value given by
Eq. (1). Riemannian manifolds are an important
class of curved manifolds, where the length is given by
the positive quadratic form
![]() ,
the most common Riemannian metric tensor is
given by the Fisher information (Amari, 1985)
,
the most common Riemannian metric tensor is
given by the Fisher information (Amari, 1985)