


Next: NORMAL DISTRIBUTION
Up: INFORMATION GEOMETRY AND NATURAL
Previous: INFORMATION GEOMETRY AND NATURAL
When applying natural gradients to approximate inference, the geometry
is defined by the approximation
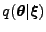 and not the full
model as usually. If the approximation
and not the full
model as usually. If the approximation
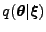 is chosen such that disjoint
groups of variables are independent, that is,
is chosen such that disjoint
groups of variables are independent, that is,
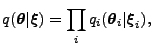 |
(5) |
the computation of the natural gradient is simplified as the Fisher
information matrix becomes block-diagonal. The required matrix
inversion can be performed very efficiently because
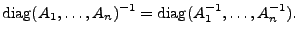 |
(6) |
The dimensionality of the problem space is often so high that
inverting the full matrix would not be feasible.
Tapani Raiko
2007-04-18
![]() and not the full
model as usually. If the approximation
and not the full
model as usually. If the approximation
![]() is chosen such that disjoint
groups of variables are independent, that is,
is chosen such that disjoint
groups of variables are independent, that is,