Iterated Extended Kalman Smoothing

In a typical NDFA learning phase, both the model parameters 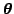$\boldsymbol{\theta}$ and the states 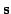$\mathbf{s}$ are updated. The updating of the network weights is computationally the most expensive part of the process, so the speed of the updating of the states is of minor importance [17]. In the control schemes studied in this work, however, the model parameters can be kept fixed and only the states are inferred. As a faster alternative to the update process used in the NDFA Matlab package, extensions of Kalman filtering [7] are explored. Kalman smoothing estimates the state of a linear Gaussian state-space model in a two-phase forward and backward pass. Extended Kalman smoothing [1] does the same for a nonlinear model by linearising the model based on the current estimate of the states and then applying linear Kalman smoothing. The process iterates between updating the states and the linearisation. Kalman-based methods are fast because they propagate information through the whole time window in every iteration, whereas the update rules included in NDFA propagate information only one step forward and backward per iteration. Unfortunately, Kalman-based methods have no guarantee of convergence when applied to nonlinear systems. To solve this issue we used iterated extended Kalman smoothing for finding a good initialisation which was then improved by some NDFA updates. In this work, a non-variational Kalman smoother is used. A variational Kalman smoother does exists [4], but as the Kalman smoother is used only for the initialisation of NDFA, the added complexity was not deemed worthwhile.