

Next: Iterated Extended Kalman Smoothing
Up: Learning Nonlinear State-Space Models
Previous: Introduction
Nonlinear State-Space Models
Nonlinear dynamical factor analysis (NDFA) [17] is a
powerful tool for modelling the dynamics of an unknown noisy
system. NDFA scales only quadratically with the dimensionality of the
observation space, so it is also suitable for modelling systems with
fairly high dimensionality [17].
In NDFA, the observations
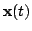 have been generated from the
hidden state
have been generated from the
hidden state
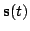 by the following generative model:
by the following generative model:
where
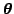 is a vector containing the model
parameters and time
is a vector containing the model
parameters and time 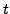 is discrete. The noise
terms
is discrete. The noise
terms
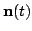 and
and
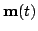 are assumed to be Gaussian and
white. Only the observations
are assumed to be Gaussian and
white. Only the observations
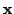 are known beforehand, and
both the states
are known beforehand, and
both the states
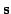 and the mappings
and the mappings
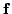 and
and
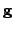 are learned from the data.
Multilayer perceptron (MLP) networks [6] suit well to
modelling both strong and mild nonlinearities. The MLP network models
for
are learned from the data.
Multilayer perceptron (MLP) networks [6] suit well to
modelling both strong and mild nonlinearities. The MLP network models
for
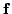 and
and
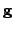 are
are
where the sigmoidal tanh nonlinearity is applied component-wise to its
argument vector. The parameters
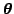 include: (1) the
weight matrices
include: (1) the
weight matrices
 , the bias vectors
, the bias vectors
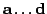 ; (2) the parameters of the distributions of
the noise signals
; (2) the parameters of the distributions of
the noise signals
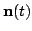 and
and
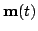 and the column
vectors of the weight matrices; (3) the hyperparameters describing the
distributions of biases and the parameters in group (2).
There are infinitely many models that can explain any given data. In
Bayesian learning, all the possible explanations are averaged
weighting by their posterior probability. The posterior probability
and the column
vectors of the weight matrices; (3) the hyperparameters describing the
distributions of biases and the parameters in group (2).
There are infinitely many models that can explain any given data. In
Bayesian learning, all the possible explanations are averaged
weighting by their posterior probability. The posterior probability
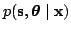 of the states and the parameters
after observing the data, contains all the relevant information about
them. Variational Bayesian learning is a way to approximate the
posterior density by a parametric distribution
of the states and the parameters
after observing the data, contains all the relevant information about
them. Variational Bayesian learning is a way to approximate the
posterior density by a parametric distribution
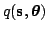 . The misfit is measured by the
Kullback-Leibler divergence:
. The misfit is measured by the
Kullback-Leibler divergence:
The approximation 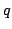 needs to be simple for mathematical tractability
and computational efficiency. Variables are assumed to depend of each
other in the following way:
needs to be simple for mathematical tractability
and computational efficiency. Variables are assumed to depend of each
other in the following way:
where 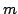 is the dimensionality of the state space
is the dimensionality of the state space
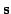 .
Furthermore,
.
Furthermore, 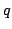 is assumed to be Gaussian.
Learning and inference happen by adjusting
is assumed to be Gaussian.
Learning and inference happen by adjusting 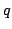 such that the cost function
such that the cost function
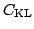 is minimised. A good initialisation and other measures are essential
because the iterative learning algorithm can easily get stuck into a
local minimum of the cost function. The standard initialisation is
based on principal component analysis of the data augmented with
embedding. Details can be found in [17].
is minimised. A good initialisation and other measures are essential
because the iterative learning algorithm can easily get stuck into a
local minimum of the cost function. The standard initialisation is
based on principal component analysis of the data augmented with
embedding. Details can be found in [17].
Subsections


Next: Iterated Extended Kalman Smoothing
Up: Learning Nonlinear State-Space Models
Previous: Introduction
Tapani Raiko
2005-05-23