Hierarchical Prior for the Weights

 The priors for weights A and B have zero mean and common variance to each dimension k, which corresponds to incoming weights of a source s_i,k:

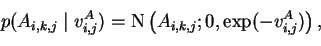$$p(A_{i,k,j}\mid v_{i,j}^{A}) = \operatorname{N}\left(A_{i,k,j};0, \exp(-v_{i,j}^{A})\right),$$ (5.7)

where A_i,k,j is the element of A_i that connects s_i+1,j to s_i,k. Parameters for B are similar and are not shown here. The variance parameter has the prior parameters that are common to dimensions j

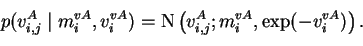$$p(v_{i,j}^{A}\mid m_{i}^{vA}, v_{i}^{vA}) = \operatorname{N}\left(v_{i,j}^A;m_{i}^{vA}, \exp(-v_{i}^{vA})\right) .$$ (5.8)

The hyperparameters m_i^vA and v_i^vA have priors of the form

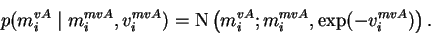$$p(m_{i}^{vA}\mid m_{i}^{mvA}, v_{i}^{mvA}) = \operatorname{N}\left(m_{i}^{vA}; m_{i}^{mvA}, \exp(-v_{i}^{mvA})\right).$$ (5.9)

The priors for these priors m_i^mvA, m_i^vvA, v_i^mvA and v_i^vvA of the hyperparameters are very flat and defined as constants in the model structure. They are of the form

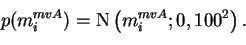$$p(m_{i}^{mvA}) = \operatorname{N}\left(m_{i}^{mvA}; 0, 100^{2}\right).$$ (5.10)