Hierarchical Prior for the Sources

The hierarchical structure of the parameters concerning the sources s and u is somewhat similar to that of the weights. The parameters are

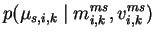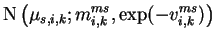$$p(\mu_{s,i,k}\mid m_{i,k}^{ms}, v_{i,k}^{ms}) \operatorname{N}\left(\mu_{s,i,k}; m_{i,k}^{ms}, \exp(-v_{i,k}^{ms})\right)$$ = (5.11)

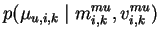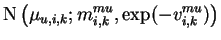$$p(\mu_{u,i,k}\mid m_{i,k}^{mu}, v_{i,k}^{mu}) \operatorname{N}\left(\mu_{u,i,k}; m_{i,k}^{mu}, \exp(-v_{i,k}^{mu})\right)$$ = (5.12)

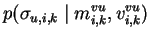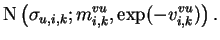$$p(\sigma_{u,i,k}\mid m_{i,k}^{vu}, v_{i,k}^{vu}) \operatorname{N}\left(\sigma_{u,i,k}; m_{i,k}^{vu}, \exp(-v_{i,k}^{vu})\right).$$ = (5.13)

The hyperparameters have priors that are common to different components k of a parameter vector

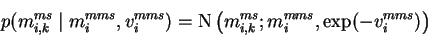$$p(m_{i,k}^{ms}\mid m_{i}^{mms}, v_{i}^{mms}) = \operatorname{N}\left(m_{i,k}^{ms}; m_{i}^{mms}, \exp(-v_{i}^{mms})\right)$$ (5.14)

and similarly for v_i,k^ms, m_i,k^mu, v_i,k^mu, m_i,k^vu and v_i,k^vu. The priors for the hyperparameters are again flat and fixed

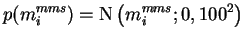$$p(m_{i}^{mms}) = \operatorname{N}\left(m_{i}^{mms}; 0, 100^{2}\right)$$ (5.15)

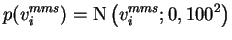$$p(v_{i}^{mms}) = \operatorname{N}\left(v_{i}^{mms}; 0, 100^{2}\right)$$ (5.16)

and so forth. The scale of the data should be made small enough as a preprocessing step.