



Next: Marginalisation Principle
Up: Bayesian Probability Theory
Previous: Bayesian Probability Theory
The Bayes rule
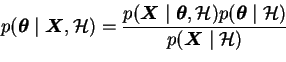 |
(3.3) |
indicates how observations change the beliefs. It is named after an
English reverend Thomas Bayes, who lived in the 18th century.
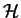 marks the prior beliefs,
X is the observed data and
marks the prior beliefs,
X is the observed data and
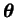 is the
parameter vector to be inferred. The term
is the
parameter vector to be inferred. The term
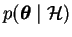 ,
the probability of the parameters given only the prior beliefs
or the probability prior to the observations is called the
prior probability. The term
,
the probability of the parameters given only the prior beliefs
or the probability prior to the observations is called the
prior probability. The term
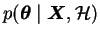 ,
the
probability of the parameters given both the observations and the
prior beliefs is called the posterior probability of the
parameters. The Bayes rule tells how the prior probability is replaced
by the posterior after getting the extra information i.e. the observed
data. The term
,
the
probability of the parameters given both the observations and the
prior beliefs is called the posterior probability of the
parameters. The Bayes rule tells how the prior probability is replaced
by the posterior after getting the extra information i.e. the observed
data. The term
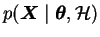 is called the
likelihood of the data and the term
is called the
likelihood of the data and the term
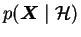 the evidence of the data.
Note that here
the evidence of the data.
Note that here 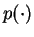 stands for a probability density function
(pdf) over a vector space.
stands for a probability density function
(pdf) over a vector space.
When inferring the parameter values
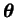 ,
the evidence term is
constant and the learning rule (
,
the evidence term is
constant and the learning rule (![[*]](cross_ref_motif.gif) ) simplifies to
) simplifies to
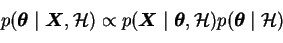 |
(3.4) |
Bayes rule tells a learning system (the player) how to update its
beliefs after observing
X. Now there is no room for 'what if',
since the posterior contains everything that can be inferred from the
observations. Note that the learning cannot start from void -
some prior beliefs are always necessary as will be discussed in
Section ![[*]](cross_ref_motif.gif) .
.




Next: Marginalisation Principle
Up: Bayesian Probability Theory
Previous: Bayesian Probability Theory
Tapani Raiko
2001-12-10
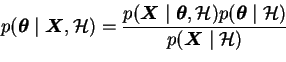
![]() ,
the evidence term is
constant and the learning rule (
,
the evidence term is
constant and the learning rule (![[*]](cross_ref_motif.gif) ) simplifies to
) simplifies to
![[*]](cross_ref_motif.gif) .
.