



Next: Approximations
Up: Bayesian Probability Theory
Previous: Bayes Rule
The marginalisation principle specifies how a learning system can
predict or generalise. The probability of observing A with prior
knowledge of B is
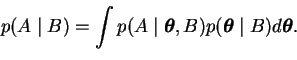 |
(3.5) |
It means that the probability of observating A can be acquired by
summing or integrating over all different explanations
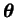 .
The term
.
The term
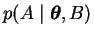 is the probability of A given a particular
explanation
is the probability of A given a particular
explanation
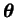 and it is weighted with the probability of the
explanation
and it is weighted with the probability of the
explanation
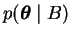 .
.
Using the principle, the evidence term can be written as
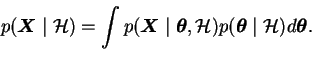 |
(3.6) |
This emphasises the role of the evidence term as a normalisation
coefficient. It is an integral over the numerator of the Bayes
rule (![[*]](cross_ref_motif.gif) ).
).
Tapani Raiko
2001-12-10
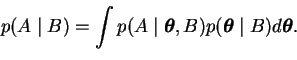
![[*]](cross_ref_motif.gif) ).
).