


Next: Summary of the updating
Up: Updating for the Gaussian
Previous: Newton iteration for the
A simple fixed-point iteration rule is obtained for the variance
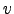 by solving the zero of the derivative:
by solving the zero of the derivative:
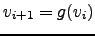 |
(57) |
In general, fixed-point iterations are stable around the solution
 if
if
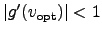 and converge best when the derivative
and converge best when the derivative
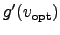 is near zero. In our case
is near zero. In our case 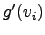 is always negative
and can be less than
is always negative
and can be less than 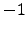 . In this case the solution can be an unstable
fixed-point. This can be avoided by taking a weighted average of
(57) and a trivial iteration
. In this case the solution can be an unstable
fixed-point. This can be avoided by taking a weighted average of
(57) and a trivial iteration
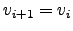 :
:
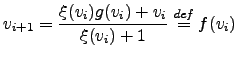 |
(58) |
The weight 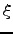 should be such that the derivative of
should be such that the derivative of 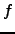 is close to
zero at the optimal solution
is close to
zero at the optimal solution
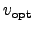 which is achieved exactly when
which is achieved exactly when
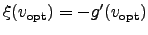 .
.
It holds
The last steps follow from the fact that
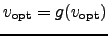 and from the
requirement that
and from the
requirement that
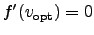 . We can assume that
. We can assume that 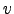 is close to
is close to
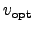 and use
and use
![$\displaystyle \xi(v) = v \left[\frac{1}{2} - V v_{\mathrm{opt}}\right] \, .$](img347.png) |
(60) |
Note that the iteration (57) can only yield estimates
with
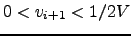 which means that
which means that
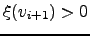 .
Therefore the use of
.
Therefore the use of 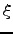 always shortens the step taken in
(58). If the initial estimate
always shortens the step taken in
(58). If the initial estimate
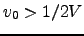 , we can
set it to
, we can
set it to
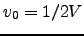 .
.



Next: Summary of the updating
Up: Updating for the Gaussian
Previous: Newton iteration for the
Tapani Raiko
2006-08-28
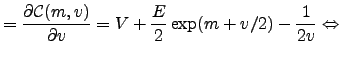
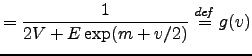
![$\displaystyle = -\frac{(E/2) \exp(m +v/2)}{\left[2V + E \exp(m+v/2)\right]^2} =...
...V - \frac{1}{2g(v)}\right] = g(v) \left[V g(v) - \frac{1}{2}\right] \Rightarrow$](img342.png)
![$\displaystyle = v_{\mathrm{opt}}\left[V v_{\mathrm{opt}}- \frac{1}{2}\right] \R...
...{\mathrm{opt}}) = v_{\mathrm{opt}}\left[\frac{1}{2} - V v_{\mathrm{opt}}\right]$](img344.png)