


Next: Fixed-point iteration for the
Up: Updating for the Gaussian
Previous: Updating for the Gaussian
The Newton iteration for 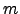 is obtained by
is obtained by
The Newton iteration converges in one step if the second derivative
remains constant. The step is too short if the second derivative
decreases and too long if the second derivative increases. For
stability, it is better to take too short than too long steps.
In this case, the second derivative always decreases if the mean 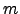 decreases
and vice versa. For stability it is therefore useful to restrict the
growth of
decreases
and vice versa. For stability it is therefore useful to restrict the
growth of 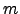 because it is consistently over-estimated.
because it is consistently over-estimated.
Tapani Raiko
2006-08-28
![]() decreases
and vice versa. For stability it is therefore useful to restrict the
growth of
decreases
and vice versa. For stability it is therefore useful to restrict the
growth of ![]() because it is consistently over-estimated.
because it is consistently over-estimated.