Training is an iterative process through time. It requires a lot of computational effort and thus is time-consuming. The training consists of drawing sample vectors from the input data set and ``teaching'' them to the SOM. The teaching consists of choosing a winner unit by the means of a similarity measure and updating the values of codebook vectors in the neighborhood of the winner unit. This process is repeated a number of times.
In one training step, one sample vector is drawn randomly from the
input data set. This vector is fed to all units in the network and a
similarity measure is calculated between the input data sample and all
the codebook vectors. The best-matching unit (BMU) is chosen to be the
codebook vector with greatest similarity with the input sample. The
similarity is usually defined by means of a distance measure. For
example in the case of Euclidean distance the best-matching unit is
the closest neuron to the sample in the input space. The Euclidean
norm of the vector 
is defined as
Then, we can define the Euclidean distance in terms of the Euclidean norm of the difference between two vectors:
The best-matching unit, usually noted as 
, is the codebook
vector that matches a given input vector best. It is defined
formally as the neuron for which
After finding the best-matching unit, units in the SOM are updated. During the update procedure, the best-matching unit is updated to be a little closer to the sample vector in the input space. The topological neighbors of the best-matching unit are also similarly updated. This update procedure streches the BMU and its topological neighbors towards the sample vector.
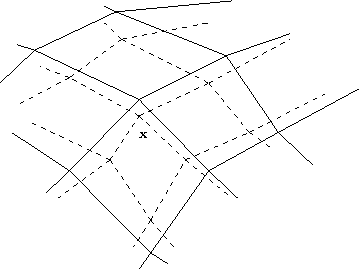
Figure 2.5: updating the best matching unit and its neighbors
In the Figure 2.5 we see an illustration of the update procedure. The codebook vectors are situated in the crossings of the solid lines. The topological relationships of the SOM are drawn with lines. The input fed to the network is marked by an x in the input space. The best-matching unit, or the winner neuron is the codebook vector closest to the sample, in this example the codebook vector in the middle above x. The winner neuron and its topological neighbors are updated by moving them a little towards the input sample. The neighborhood in this case consists of the eight neighboring units in the figure. The updated network is shown in the same figure with dashed lines.
The computational effort consists of finding a best-matching unit among all the neurons and updating the codebook vectors in the neighborhood of the winner unit. If the neighborhood is large, there are a lot of codebook vectors to be updated. This is the case in the beginning of the training process, where it is recommended to use large neighborhoods. In the case of large networks, relatively larger portion of the time is spent looking for a winner neuron. All these considerations depend on the time spent on each of these phases depending on particular software and hardware used.