If SOMs were adopted on a large scale for summarizing information in various data sets, it might be of use to be able to compare the data sets indirectly by comparing the ``summaries'' formed by the ordered sets of reference vectors. Possible application areas could include the comparison of organizational data (``data warehousing'', making data on an organization or company available for on-line retrieval is nowadays quite popular, cf. Fayyad et al., 1996c) and comparison of the expertise of different parties for deciding what they could learn from each other.
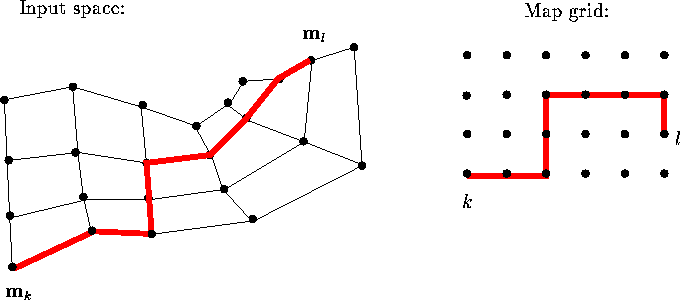
Figure 7: The nonlinearity of the SOM is taken into account by defining
the distance between map units to be the distance along the
``elastic network'' formed of the map in the input space. On the
left the reference vectors of a two-dimensional map in a
two-dimensional input space have been denoted by dots. Neighboring
reference vectors have been connected with thin lines. Distance
between units k and l is drawn with the thick line. Depending on
the values of the reference vectors the path along which the
distance is computed need not be the shortest path on the map grid,
as shown on the right.
Such comparisons of different maps should focus on the ``equivalence of use'', or similarity of the representations of knowledge the maps form. A measure of the similarity of two maps based on how they represent relations between data items has been presented in Publication 7. The relation, here the distance, between the representations of two data items on the map display is computed taking into account the nonlinearity of the map: the distance between each pair of neighboring map units is first defined to be the distance of the corresponding reference vectors. The distance of any two map units is defined to be the distance along the minimum path from one of the units to the other, along the map (cf. Kraaijveld et al., 1992; Kraaijveld et al., 1995). The computation of the distance is illustrated in Figure 7. The distance between any two data items is then defined to be the sum of the distances from each of the data items to the closest reference vector, plus the distance between the corresponding units on the map. The measure of the (dis)similarity of two maps, a metric for SOMs, can then be constructed by comparing the relations of pairs of data items on the two maps.