Since the SOM learning process described in Section 6.4.1 is stochastic, there will be some variation left in the learning results. Thus, to ensure good quality several maps can be computed and the best map can be chosen according to the cost function, Equation 7.
The cost function of the SOM is specific to the size of the map and to the topology of the map lattice, which is defined by the neighborhood kernel. The value of the cost function will generally decrease as the map size increases, and increase as the width of the neighborhood function increases. Thus, it cannot be used to compare maps with different sizes or neighborhood kernels; some auxiliary criteria are therefore needed.
A measure of how well a map preserves the topology of the input space
might be a suitable auxiliary criterion of map goodness. Topology
preservation has, however, turned out to be quite difficult to define
sensibly for a discrete grid. There seem to exist two different
approaches for measuring the degree of topology preservation (specific
examples have been reviewed in Publication 7;
additional approaches have been proposed at least by Zrehen,
1993; and Hämäläinen, 1994). In
the first approach the relations between the reference vectors and the
relations between the corresponding units on the map lattice are
compared. For example, it can be measured how often the line
connecting the reference vectors of neighboring units will be
dissected by the Voronoi region of some other unit than the endpoints
[Zrehen, 1993]. The Voronoi region of unit i is defined to be the set
consisting of the points in the input space that are closer to 
than to any other reference vector.
An alternative approach for measuring topology preservation is to use input samples to determine how continuous the mapping from the input space to the map grid is. If the two reference vectors that are closest to a given data item are not neighbors on the map lattice, then the mapping is not continuous near that item.
Neither of these approaches takes into account the accuracy of the map in representing the data, the first term in the decomposition of the cost function (Eq. 9). In Publication 7 it is proposed that the goodness of the SOM could be measured by using a sum of the accuracy and a suitably chosen index of the topology preservation (cf. Fig. 6).
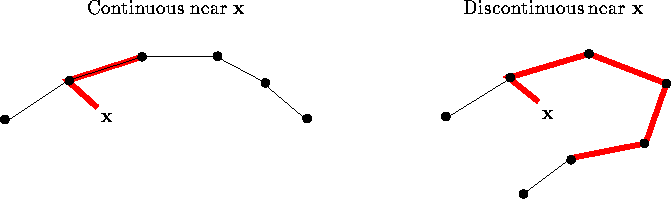
Figure 6: One method for measuring the goodness of SOMs consists of
computing, for a representative set of input samples 
, the
distance from first to the closest reference vector, and
thereafter to the second-closest reference vector along the map. The
index of goodness is the average of these distances. If the mapping
from the input space to the map grid is continuous near
the distances are generally smaller than when the mapping is
discontinuous. The dots denote reference vectors of a
one-dimensional map in a two-dimensional input space. Reference
vectors of neighboring map units have been connected with thin
lines. The thick line indicates how the distance is computed. For
two-dimensional maps the distance is computed using the shortest
path along the map.
A related measure has been proposed by Minamimoto et al. (1995) for analyzing the topological structure of the data space. There are two essential differences between the measures, however: first, Minamimoto et al. combine qualitatively different measures using a linear combination. The coefficients of the combination may then be difficult to choose, whereas in Publication 7 the measures that are combined measure distances in the same space. Second, Minamimoto et al. also combine the number of reference vectors in the measure. We, however, considered the size of the map only indirectly, to the extent that is contributes to the preservation of the topology.
The best way to use the measure of goodness for choosing a map, assuming there are enough computational resources, seems to be to teach a set of maps with each choice of the map size and the neighborhood kernel. The map that minimizes the cost function (Eq. 7) is then chosen from each set. Of the resulting set of best maps, the final map is chosen according to the measure of goodness presented in Publication 7.
Some additional notes, for which there was no space in Publication 7, are given below: