



Next: Variance modelling
Up: Variational learning of nonlinear
Previous: Control
Contents
Bayes Blocks for nonlinear Bayesian networks
Nonlinear factor analysis and nonlinear state-space models can be seen
as special cases of Bayesian networks where the linearity assumption
is relaxed. Aside from these two, there are lots of possibilities to
build the model structure that defines the dependencies between the
parameters and the data. To be able to manage the variety, a modular
software package using C++/Python called the Bayes
Blocks (Valpola et al., 2003a) has been created. It is introduced in
Publication I and in an earlier conference paper by
Valpola et al. (2001).
The design principles for Bayes Blocks have been the following.
Firstly, we use standardised building blocks that can be connected
rather freely and can be learned with local learning rules, i.e. each
block only needs to communicate with its neighbours. Secondly, the
system should work with very large scale models.
Computational complexity is linear with respect to the number of data
samples and connections in the model.
The building blocks include Gaussian variables, summation,
multiplication, and nonlinearity. The framework does not make much difference in
parameters
 and latent variables
and latent variables
 , the former are
represented with scalars and the latter as vectors. Variational
Bayesian learning provides a cost function which can be used for
updating the variables as well as optimising the model structure. The
derivation of the cost function, as well as learning and inference
rules, is automatic which means that the user only needs to define the
connections between the blocks.
, the former are
represented with scalars and the latter as vectors. Variational
Bayesian learning provides a cost function which can be used for
updating the variables as well as optimising the model structure. The
derivation of the cost function, as well as learning and inference
rules, is automatic which means that the user only needs to define the
connections between the blocks.
The Gaussian node is a variable node and the basic element in building
hierarchical models. Figure 4.4 (leftmost subfigure)
shows the schematic diagram of the Gaussian node. Its output is the
value of a Gaussian random variable  , which is conditioned by the
inputs
, which is conditioned by the
inputs  and
and  . Denote generally by
. Denote generally by
 the
probability density function of a Gaussian random variable
the
probability density function of a Gaussian random variable  having
the mean
having
the mean  and variance
and variance
 . Then the conditional
probability function of the variable
. Then the conditional
probability function of the variable  is
is
 . As a generative model, the Gaussian node takes
its mean input
. As a generative model, the Gaussian node takes
its mean input  and adds to it Gaussian noise (or innovation) with
variance
and adds to it Gaussian noise (or innovation) with
variance  .
.
Figure 4.4:
First subfigure from the left: The circle represents a
Gaussian node corresponding to the latent variable  conditioned by
mean
conditioned by
mean  and variance
and variance  . Second subfigure:
Addition and multiplication nodes are used to form an affine
mapping from
. Second subfigure:
Addition and multiplication nodes are used to form an affine
mapping from  to
to  . Third subfigure: A nonlinearity
. Third subfigure: A nonlinearity
 is applied immediately after a Gaussian variable. The
rightmost subfigure: Delay operator delays a time-dependent signal
by one time unit.
is applied immediately after a Gaussian variable. The
rightmost subfigure: Delay operator delays a time-dependent signal
by one time unit.
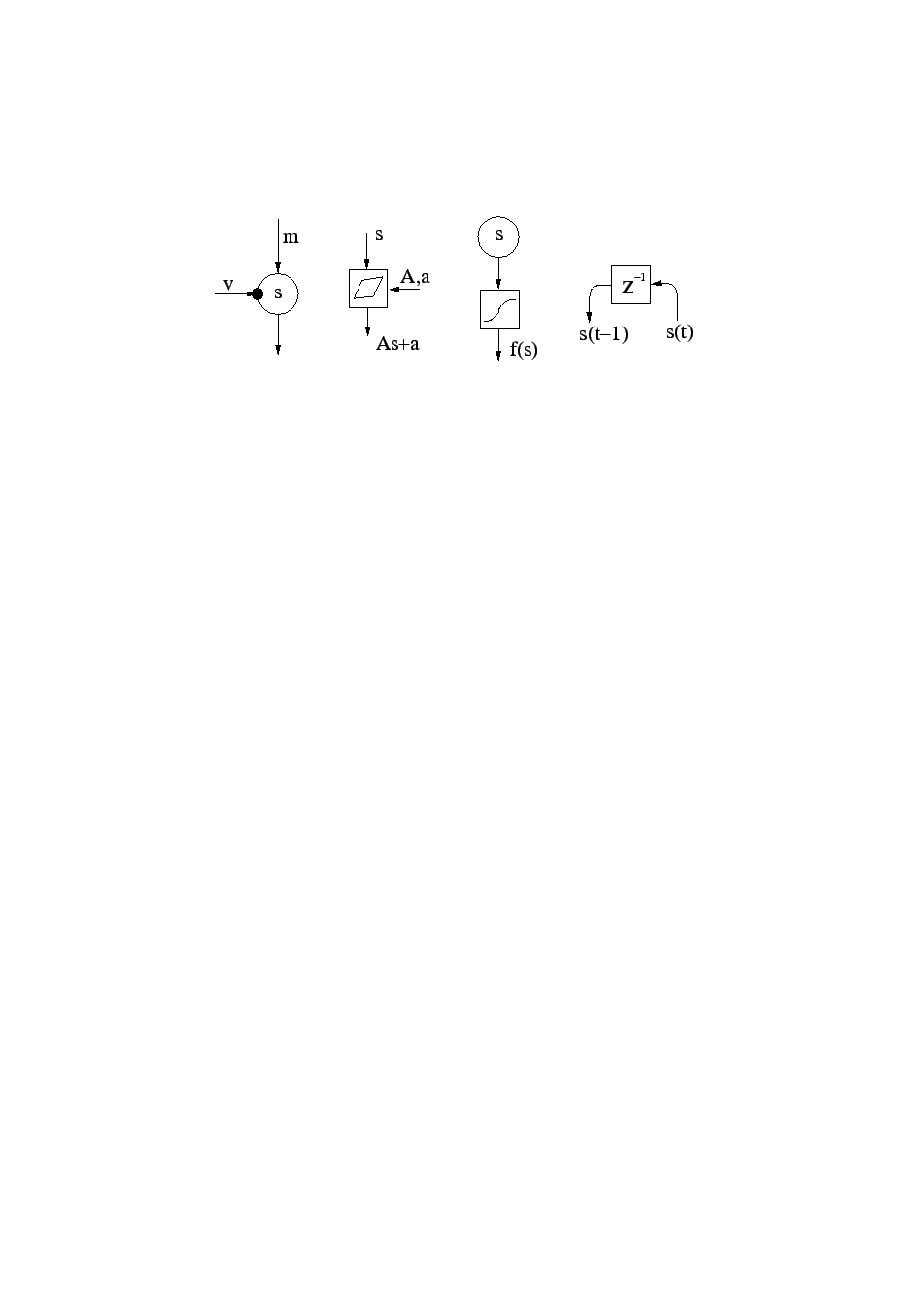 |
The addition and multiplication nodes are used for summing and
multiplying variables. These standard mathematical operations are
typically used to construct linear mappings between the variables. A
nonlinear computation node can be used for constructing nonlinear
mappings between the variable nodes. The delay operation can be used
to model dynamics. Harva et al. (2005) implements several new blocks
including mixture-of-Gaussians and rectified Gaussians.
Harva and Kabán (2005) use the rectified Gaussian node to create a factor
model with non-negativity constraints and
Nolan et al. (2006) applies Bayes Blocks in an astronomical problem.
Nodes propagate certain expectations about their state to their
neighbours in the network. For variable nodes in a network, update
rules for the posterior approximation  that minimise the cost
function
that minimise the cost
function
 given that
given that  of all the other variables stays
constant, have been derived. The updates are very simple since the
posterior approximation
of all the other variables stays
constant, have been derived. The updates are very simple since the
posterior approximation  is of a very simple form: It is a Gaussian
with a diagonal covariance matrix.
is of a very simple form: It is a Gaussian
with a diagonal covariance matrix.
Winn and Bishop (2005) introduce an algorithm called variational message
passing with close similarities with Bayes Blocks.
It does not allow for nonlinearities or variance modelling (see the following
section), but on the other hand, it handles discrete variables more
freely. It also allows for a posterior approximation factorised such that
disjoint groups of variables are independent, but dependencies within
the group are modelled. Variational message passing updates the
posterior approximation of one factor at a time using VB learning.
Note that the best properties of Bayes Blocks and variational message passing could be
combined.
Similar models can be studied also with rather different posterior
approximations. Spiegelhalter et al. (1995) introduce the BUGS
software package that uses Gibbs sampling (see Section 2.5.4)
for Bayesian inference. The package supports mixture models,
nonlinearities, and non-stationary variance. A thorough experimental
comparison to Bayes Blocks would be very valuable.
Subsections




Next: Variance modelling
Up: Variational learning of nonlinear
Previous: Control
Contents
Tapani Raiko
2006-11-21
 and latent variables
and latent variables
 , the former are
represented with scalars and the latter as vectors. Variational
Bayesian learning provides a cost function which can be used for
updating the variables as well as optimising the model structure. The
derivation of the cost function, as well as learning and inference
rules, is automatic which means that the user only needs to define the
connections between the blocks.
, the former are
represented with scalars and the latter as vectors. Variational
Bayesian learning provides a cost function which can be used for
updating the variables as well as optimising the model structure. The
derivation of the cost function, as well as learning and inference
rules, is automatic which means that the user only needs to define the
connections between the blocks.
 , which is conditioned by the
inputs
, which is conditioned by the
inputs  and
and  . Denote generally by
. Denote generally by
 the
probability density function of a Gaussian random variable
the
probability density function of a Gaussian random variable  having
the mean
having
the mean  and variance
and variance
 . Then the conditional
probability function of the variable
. Then the conditional
probability function of the variable  . As a generative model, the Gaussian node takes
its mean input
. As a generative model, the Gaussian node takes
its mean input  .
.
 . Third subfigure: A nonlinearity
. Third subfigure: A nonlinearity
 is applied immediately after a Gaussian variable. The
rightmost subfigure: Delay operator delays a time-dependent signal
by one time unit.
is applied immediately after a Gaussian variable. The
rightmost subfigure: Delay operator delays a time-dependent signal
by one time unit.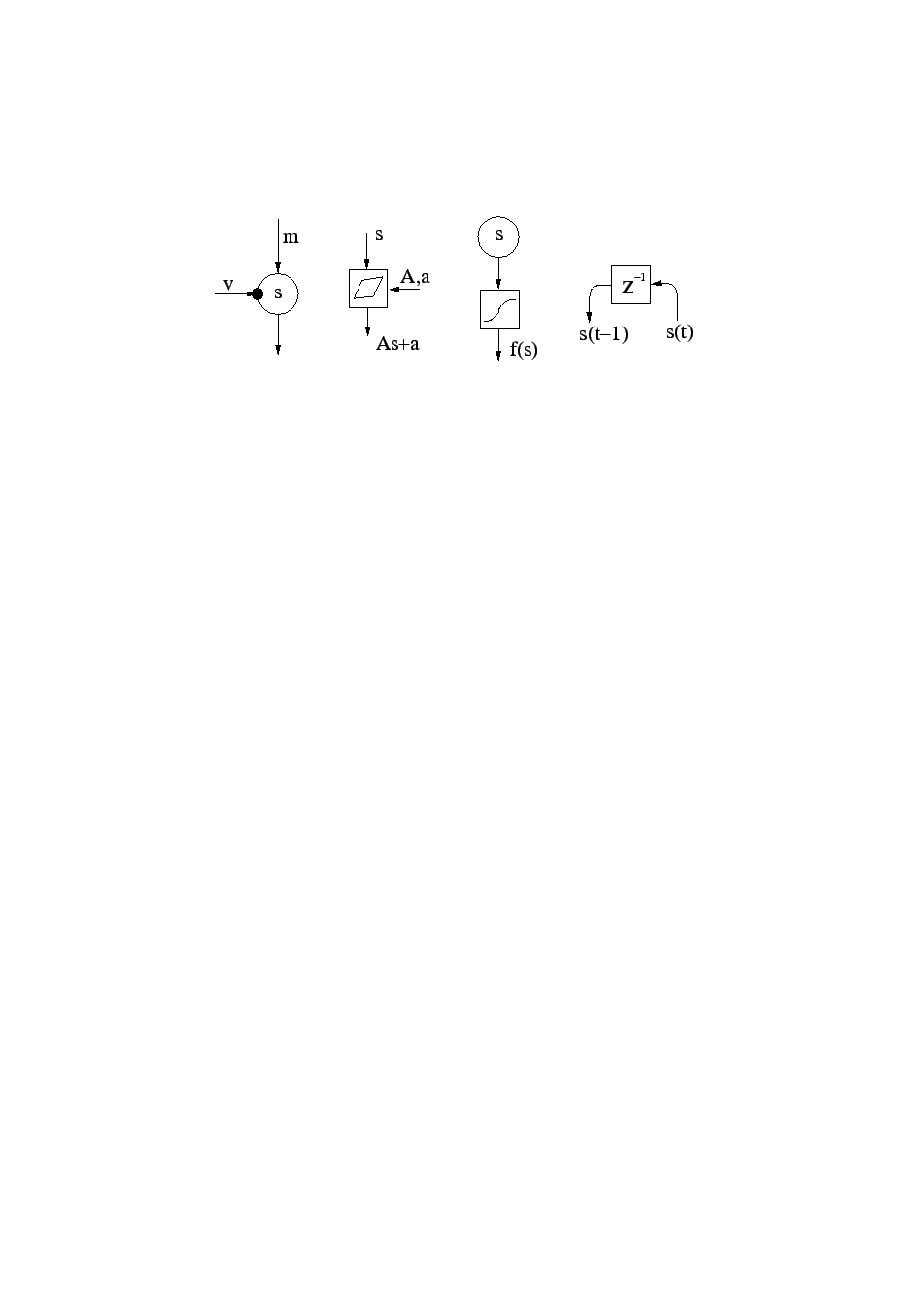
 that minimise the cost
function
that minimise the cost
function
 given that
given that