


Next: Overfitting
Up: Principal Component Analysis with
Previous: Adapting the EM Algorithm
Adapting the Subspace Learning Algorithm
The subspace learning algorithm works in a straightforward manner also in the
presence of missing values. We just take the sum over only those
indices 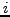 and
and 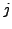 for which the data entry
for which the data entry 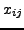 (the
(the 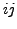 th
element of
th
element of
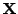 ) is observed, in short
) is observed, in short
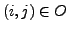 . The cost function is
. The cost function is
and its partial derivatives are
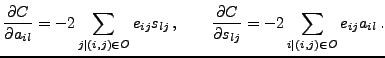 |
(11) |
The update rules for gradient descent are
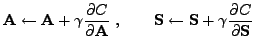 |
(12) |
and the update rules for natural gradient descent are
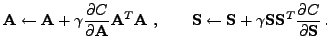 |
(13) |
We propose a novel speed-up to the original simple gradient descent algorithm.
In Newton's method for optimization, the gradient is multiplied by the
inverse of the Hessian matrix. Newton's method is known to converge fast
especially in the vicinity of the optimum, but using the full Hessian is
computationally too demanding in truly high-dimensional problems.
Here we use only the diagonal part of the Hessian matrix.
We also include a control parameter 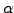 that allows the learning
algorithm to interpolate between the standard gradient descent (
that allows the learning
algorithm to interpolate between the standard gradient descent (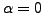 ) and the diagonal
Newton's method (
) and the diagonal
Newton's method (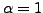 ), much like the Levenberg-Marquardt algorithm.
The learning rules then take the form
), much like the Levenberg-Marquardt algorithm.
The learning rules then take the form
The computational complexity is 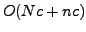 per iteration.
per iteration.



Next: Overfitting
Up: Principal Component Analysis with
Previous: Adapting the EM Algorithm
Tapani Raiko
2007-09-11
![]() and
and ![]() for which the data entry
for which the data entry ![]() (the
(the ![]() th
element of
th
element of
![]() ) is observed, in short
) is observed, in short
![]() . The cost function is
. The cost function is
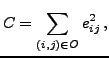 with
with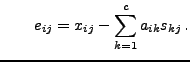
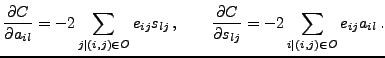
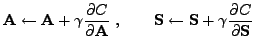
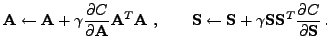
![]() that allows the learning
algorithm to interpolate between the standard gradient descent (
that allows the learning
algorithm to interpolate between the standard gradient descent (![]() ) and the diagonal
Newton's method (
) and the diagonal
Newton's method (![]() ), much like the Levenberg-Marquardt algorithm.
The learning rules then take the form
), much like the Levenberg-Marquardt algorithm.
The learning rules then take the form