When updates are done locally,
information spreads around slowly because the states of different time
slices affect each other only between updates. It is possible to
predict this interaction by a suitable approximation. We get a novel
update algorithm for the posterior mean of the states by replacing
partial derivatives of the cost function w.r.t. state means
![]() by
(approximated) total derivatives
by
(approximated) total derivatives
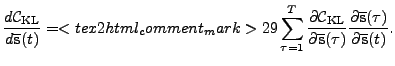 |
(6) |
Before going into details, let us go through the idea. The posterior
distribution of the state
![]() can be factored into three
potentials, one from
can be factored into three
potentials, one from
![]() (the past), one from
(the past), one from
![]() (the
future), and one from
(the
future), and one from
![]() (the observation). We will linearise
the nonlinear mappings so that the three potentials become
Gaussian. Then also the posterior of
(the observation). We will linearise
the nonlinear mappings so that the three potentials become
Gaussian. Then also the posterior of
![]() becomes Gaussian with a
mean that is the weighted average of the means of the three
potentials, where the weights are the inverse (co)variances of the
potentials. A change in the mean of a potential results in a change
of the mean of the posterior inversely proportional to their
(co)variances.
becomes Gaussian with a
mean that is the weighted average of the means of the three
potentials, where the weights are the inverse (co)variances of the
potentials. A change in the mean of a potential results in a change
of the mean of the posterior inversely proportional to their
(co)variances.
The terms of the cost function (See Equation (5.6) in
[1], although the notation is somewhat different)
that relate to
![]() are
are
| (8) | ||
| (9) |
| (10) | ||
| (11) | ||