


Next: Inference Methods
Up: State Inference in Variational
Previous: Introduction
Nonlinear State-Space Models
In nonlinear state-space models, the observation vectors
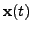 ,
,
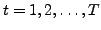 , are assumed to have been generated from
unobserved state (or source) vectors
, are assumed to have been generated from
unobserved state (or source) vectors
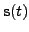 .
The model equations are
.
The model equations are
Both the mixing mapping
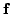 and the process mapping
and the process mapping
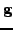 are
nonlinear. The noise model for both mixing and dynamical process is often
assumed to be Gaussian
are
nonlinear. The noise model for both mixing and dynamical process is often
assumed to be Gaussian
where
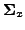 and
and
 are the noise covariance matrices. In blind source
separation, the mappings
are the noise covariance matrices. In blind source
separation, the mappings
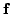 and
and
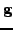 are assumed to be unknown
[1] but in this paper we concentrate on the case where
they are known.
are assumed to be unknown
[1] but in this paper we concentrate on the case where
they are known.
Subsections
Tapani Raiko
2005-12-08
![]() ,
,
![]() , are assumed to have been generated from
unobserved state (or source) vectors
, are assumed to have been generated from
unobserved state (or source) vectors
![]() .
The model equations are
.
The model equations are