Experiments

The goal is to study nonlinear models by measuring the quality of reconstructions of missing values.

Figure 1: Some speech data with and without missing values and the reconstruction given by HNFA.

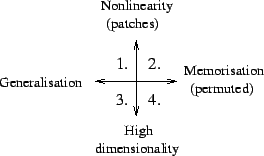
The data set consists of speech spectrograms from several Finnish subjects. Short term spectra are windowed to 30 dimensions with a standard preprocessing procedure for speech recognition. It is clear that a dynamic³ source model would give better reconstructions, but in this case the temporal information is left out to ease the comparison of the models. Half of the about 5000 samples are used as test data with some missing values. Missing values are set in four different ways to measure different properties of the algorithms (Figure 2):

1. 38 percent of the values are set to miss randomly in $4 \times 4$ patches. (Figure 1)
   
2. Training and testing sets are randomly permuted before setting missing values in $4 \times 4$ patches as in Setting 1.
   
3. 10 percent of the values are set to miss randomly independent of any neighbours. This is an easier setting, since simple smoothing using nearby values would give fine reconstructions.
   
4. Training and testing sets are permuted and 10 percent of the values are set to miss independently of any neighbours.
   

Figure 2: Four different experimental settings with the speech data used for measuring different properties of the algorithms.

We tried to optimise each method and in the following, we describe how we got the best results. The SOM was run using the SOM Toolbox with long learning time, 2500 map units and random initialisations. One parameter, the width of the softening kernels [2] that was used in making the reconstruction, was selected based on the results, which is not completely fair. In other methods, the optimisation was based on minimising the cost function (2) or its approximation. NFA was learned for 5000 sweeps through data using a Matlab implementation. Varying number of sources were tried out and the best ones were used as the result. The optimal number of sources was around 12 to 15 and the size used for the hidden layer was 30. A large enough number should do, since the algorithm can effectively prune out parts that are not needed. Some runs with a higher number of sources were good according to the approximation of the cost function (2), but a better approximation or a simple look at the reconstruction error of the observed data showed that those runs were actually bad. These runs and the ones that diverged were filtered out.

The details of the HNFA (and FA) implementation can be found in [1]. In FA, the number of sources was 28. In HNFA, the number of sources at the top layer was varied and the best runs according to the cost function were selected. In those runs, the size of the top layer varied from 6 to 12 and the size of the middle layer, which is determined during learning, turned out to vary from 12 to 30. HNFA was run for 5000 sweeps through data. Each run with NFA or HNFA takes about 8 hours of processor time, while FA and SOM are faster.

Several runs were conducted with different random initialisations but the same data and the same missing value pattern for each setting and for each method. The number of runs in each cell is about 30 for HNFA, 4 for NFA and 20 for the SOM. FA always converges to the same solution. The mean and the standard deviation of the mean square reconstruction error are:

	FA	HNFA	NFA	SOM
1.	$1.87$	$1.80 \pm 0.03$	$1.74 \pm 0.02$	$1.69 \pm 0.02$
2.	$1.85$	$1.78 \pm 0.03$	$1.71 \pm 0.01$	$1.55 \pm 0.01$
3.	$0.57$	$0.55 \pm .005$	$0.56 \pm .002$	$0.86 \pm 0.01$
4.	$0.58$	$0.55 \pm .008$	$0.58 \pm .004$	$0.87 \pm 0.01$

The order of results of the Setting 1 follow our expectations on the nonlinearity of the models. The SOM with highest nonlinearity gives the best reconstructions, while NFA, HNFA and finally FA follow in that order. The results of HNFA vary the most - there is potential to develop better learning schemes to find better solutions more often. The sources $\mathbf{h}(t)$ of the hidden layer did not only emulate computational nodes, but they were also active themselves. Avoiding this situation during learning could help to find more nonlinear and thus perhaps better solutions.

In the Setting 2, due to the permutation, the test set contains vectors very similar to some in the training set. Therefore, generalisation is not as important as in the Setting 1. The SOM is able to memorise details corresponding to individual samples better due to its high number of parameters. Compared to the Setting 1, SOM benefits a lot and makes clearly the best reconstructions, while the others benefit only marginally.

The Settings 3 and 4, which require accurate expressive power in high dimensionality, turned out not to differ from each other much. The basic SOM has only two intrinsic dimensions⁴ and therefore it was clearly poorer in accuracy. Nonlinear effects were not important in these settings, since HNFA and NFA were only marginally better than FA. HNFA was better than NFA perhaps because it has more latent variables when counting both $\mathbf{s}(t)$ and $\mathbf{h}(t)$.

To conclude, HNFA lies between FA and NFA in performance. HNFA is applicable to high dimensional problems and the middle layer can model part of the nonlinearity without increasing the computational complexity dramatically. FA is better than the SOM when expressivity in high dimensions is important, but the SOM is better when nonlinear effects are more important. The extensions of FA, NFA and HNFA, expectedly performed better than FA in each setting. HNFA is recommended over NFA because of its reliability. It may be possible to enhance the performance of NFA and HNFA by new learning schemes whereas especially FA is already at its limits. On the other hand, FA is best if low computational complexity is the determining factor.