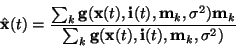 |
(1) |
A self-organising map, which is used to reconstruct missing values, is called the Supervised SOM [5]. Model vectors lie in the same space as the data. Here we use a variant in which each data vector is matched to model vectors ignoring the values that are missing. In the learning phase, the winning model vector and its neighbours in the map are moved slightly towards the data vector ignoring the dimensions of the missing values again. Finally the reconstructions of the missing values are combinations of the values from the model vectors, which are weighted according to Gaussian kernels assigned to them:
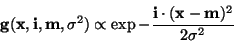 |
(2) |
x(t) is a data vector and
![]() its
reconstruction.
i(t) indicates which values are
observed.
mi is a model vector. Parameter
its
reconstruction.
i(t) indicates which values are
observed.
mi is a model vector. Parameter ![]() is
called the width of the softening kernels. When
is
called the width of the softening kernels. When ![]() approaches
zero, the reconstruction approaches the single winning model vector.
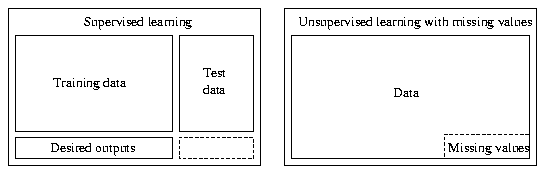
The data set might contain missing values in each of the vectors, but
the model vectors contain no missing values.
approaches
zero, the reconstruction approaches the single winning model vector.
The data set might contain missing values in each of the vectors, but
the model vectors contain no missing values.
The reconstructions are restricted to convex combinations of the model vectors. This might be significant, when the true dimensionality of the data is large and most of the data is on the border: When a three dimensional ball loses 5 percent of its radius, it loses about 14 percent of its mass, but a 50 dimensional ball loses more than 92 percent of its mass.
 |