The Self-Organizing Map is one of the most popular neural network models. It belongs to the category of competitive learning networks. The Self-Organizing Map is based on unsupervised learning, which means that no human intervention is needed during the learning and that little needs to be known about the characteristics of the input data. We could, for example, use the SOM for clustering data without knowing the class memberships of the input data. The SOM can be used to detect features inherent to the problem and thus has also been called SOFM, the Self-Organizing Feature Map.
The Self-Organizing Map was developed by professor Kohonen [20]. The SOM has been proven useful in many applications [22]. For closer review of the applications published in the open literature, see section 2.3.
The SOM algorithm is based on unsupervised, competitive learning. It provides a topology preserving mapping from the high dimensional space to map units. Map units, or neurons, usually form a two-dimensional lattice and thus the mapping is a mapping from high dimensional space onto a plane. The property of topology preserving means that the mapping preserves the relative distance between the points. Points that are near each other in the input space are mapped to nearby map units in the SOM. The SOM can thus serve as a cluster analyzing tool of high-dimensional data. Also, the SOM has the capability to generalize. Generalization capability means that the network can recognize or characterize inputs it has never encountered before. A new input is assimilated with the map unit it is mapped to.
The Self-Organizing Map is a two-dimensional array of neurons:
![]()
This is illustrated in Figure 2.3. One neuron is a vector called the codebook vector
![]()
This has the same dimension as the input vectors (n -dimensional). The neurons are connected to adjacent neurons by a neighborhood relation. This dictates the topology, or the structure, of the map. Usually, the neurons are connected to each other via rectangular or hexagonal topology. In the Figure 2.3 the topological relations are shown by lines between the neurons.
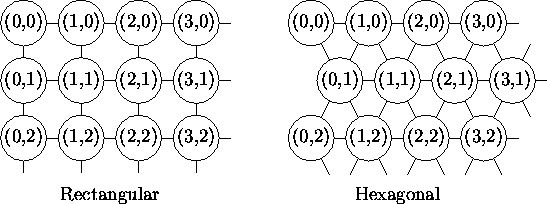
Figure 2.3: Different topologies
One can also define a distance between the map units according to
their topology relations. Immediate neighbors (the neurons that are
adjacent) belong to the neighborhood ![]() of the neuron
of the neuron ![]() .
The neighborhood function should be a decreasing function of time:
.
The neighborhood function should be a decreasing function of time:
![]() . Neighborhoods of different sizes in a hexagonal
lattice are illustrated in Figure 2.4. In the smallest
hexagon, there are all the neighbors belonging to the smallest
neighborhood of the neuron in the middle belonging to a hexagonal
lattice. The topological relations between the neurons are left out
for clarity.
. Neighborhoods of different sizes in a hexagonal
lattice are illustrated in Figure 2.4. In the smallest
hexagon, there are all the neighbors belonging to the smallest
neighborhood of the neuron in the middle belonging to a hexagonal
lattice. The topological relations between the neurons are left out
for clarity.
In the basic SOM algorithm, the topological relations and the number of neurons are fixed from the beginning. This number of neurons determines the scale or the granularity of the resulting model. Scale selection affects the accuracy and the generalization capability of the model. It must be taken into account that the generalization and accuracy are contradictory goals. By improving the first, we lose on the second, and vice versa.
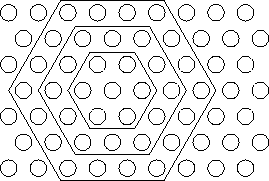
Figure 2.4: Neighborhood of a given winner unit