The neighborhood function includes the learning rate function ![]() which is a decreasing function of time and the function that
dictates the form of the neighborhood function. The form of the latter
function also determines the rate of change around the winner unit.
The neighborhood function can be written as
which is a decreasing function of time and the function that
dictates the form of the neighborhood function. The form of the latter
function also determines the rate of change around the winner unit.
The neighborhood function can be written as
![]()
in the
case of the Gaussian neighborhood function around the winner neuron
![]() .
.
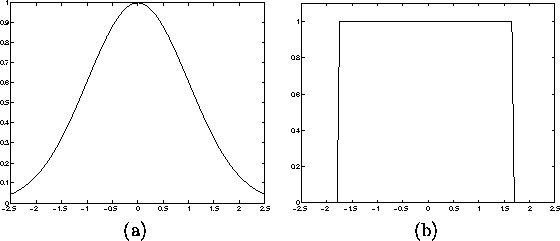
Figure 2.6: Neighborhood function values
A variety of neighborhood functions can be used. We can constrain the
neigbourhood function to be non-increasing around the winner unit
![]() . Thus, the neighborhood function can also be constant
around the winner unit. One choice for a neighborhood function is to
use a Gaussian kernel around the winner neuron as described above.
This is computationally demanding as the exponential function has
to be calculated, but can well be approximated by the ``bubble''
neighborhood function. The bubble neighborhood function is a constant
function in the defined neighborhood of the winner neuron, that is,
every neuron in the neighborhood is updated the same proportion of the
difference between the neuron and the presented sample vector. The
bubble neighborhood function is a good compromise between the
computational cost and the approximation of the Gaussian.
. Thus, the neighborhood function can also be constant
around the winner unit. One choice for a neighborhood function is to
use a Gaussian kernel around the winner neuron as described above.
This is computationally demanding as the exponential function has
to be calculated, but can well be approximated by the ``bubble''
neighborhood function. The bubble neighborhood function is a constant
function in the defined neighborhood of the winner neuron, that is,
every neuron in the neighborhood is updated the same proportion of the
difference between the neuron and the presented sample vector. The
bubble neighborhood function is a good compromise between the
computational cost and the approximation of the Gaussian.
In the Figure 2.6 the two used forms of the neighborhood function are illustrated. In the left, we see the form of a Gaussian (a), on the right the bubble function (b).