Neural network interpretation of the model

It is somewhat artificial to call the linear factor analysis model a neural network, but it serves as a good starting point for the later development. The structure of neural networks is usually represented graphically by showing the computational elements, neurons, of the network. Each node corresponds to one neuron and the arrows usually denote weighted sums of the values from other neurons. It should be noted that although this representation bears resemblance to graphical models, a graphical model represents the conditional dependences while the neural network representation shows the computational structure. In general, these representations are therefore different.

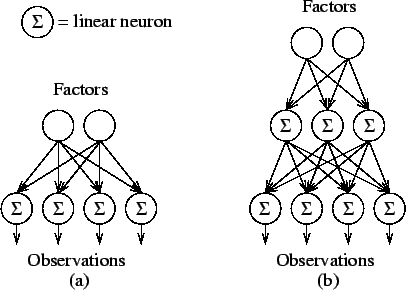
The linear factor analysis model can be represented as a neural network with two layers. On the first layer there are the factors and the second layer consists of linear neurons which compute a weighted sum of their inputs. A network interpretation of a model with two-dimensional factors and four-dimensional observations is depicted schematically in figure 5a. The weights A_ij are shown as links between the nodes but the biases a_i are not shown.

  

Figure 5: (a) The linear factor analysis model can be interpreted as a neural network with one layer of linear neurons. The arrows represent connections with weights A_ij attached to them. (b) A multi-layer structure can be replaced by a single layer of linear neurons.

Linear neurons as building blocks for larger networks are too simplistic because adding extra layers of linear neurons does not increase the representational power of the network. This is easily seen by considering the model

x(t) = B (A s(t) + a) + b + n(t), (29)

shown in figure 5b. By setting A' = BA and a' = Ba + b the model can be written as

x(t) = A' s(t) + a' + n(t), (30)

which, interpreted as a neural network, has only one layer of linear neurons.