


Next: Specification of the model
Up: Ensemble learning
Previous: Cost function
The minimum message length encoding, which was discussed in
section 4.3.2, is not decodable, that is, it is not sufficient
to actually find x. This is because in order to decode 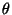 ,
the receiver should know the precision
,
the receiver should know the precision
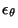 in addition
to the prior knowledge
in addition
to the prior knowledge 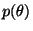 , but
, but
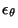 was not
included in the message. In [131], Wallace and Freeman
argued that the values and the accuracies of the parameters are not
independent, and one can construct a decodable message with almost the
same code length as in minimum message length coding.
was not
included in the message. In [131], Wallace and Freeman
argued that the values and the accuracies of the parameters are not
independent, and one can construct a decodable message with almost the
same code length as in minimum message length coding.
Later Hinton and van Camp introduced a ``bits-back'' argument to show
that by a clever coding scheme, a decodable message is obtained
without encoding
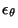 [44]. The sender
uses the following coding scheme:
[44]. The sender
uses the following coding scheme:
- 1.
- Compute a distribution
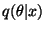 based on the observation
x (the algorithm for doing this is defined later).
based on the observation
x (the algorithm for doing this is defined later).
- 2.
- Pick
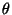 from the distribution
from the distribution
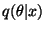 and encode
it with a very high prespecified precision (
and encode
it with a very high prespecified precision (
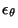 is
close to zero) using
is
close to zero) using 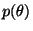 .
.
- 3.
- Encode x using the encoded
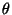 and
and
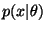 .
.
It would seem that the sender has had to use a very large number of
bits, because the length of the first part
![\begin{displaymath}L(\theta) = -\int q(\theta \vert x) \log [p(\theta) \epsilon_\theta] d\theta
\end{displaymath}](img63.gif) |
(17) |
is very high due to small
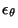 . It turns out that this
is not the case, however. The trick is that in step 2, the sender can
encode a secondary message in the choice of
. It turns out that this
is not the case, however. The trick is that in step 2, the sender can
encode a secondary message in the choice of 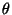 . The average
length of this message is
. The average
length of this message is
![\begin{displaymath}L(\theta \vert q) = - \int q(\theta \vert x) \log [q(\theta \vert x)
\epsilon_\theta] d\theta.
\end{displaymath}](img64.gif) |
(18) |
Although the length of the first part of the message is very high,
most of it is actually used by the secondary message. In the end, the
receiver will get those bits back, so to say, and hence the name
bits-back argument. The total length of the part which is used for
encoding x is
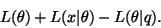 |
(19) |
It might not be immediately clear that the receiver can decode the
secondary message hidden in the choice of 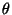 . In the receiving
end, the decoding proceeds as follows:
. In the receiving
end, the decoding proceeds as follows:
- 1.
- Decode
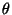 from the first part of the message using
from the first part of the message using 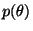 .
.
- 2.
- Decode x from the second part of the message using
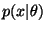 .
.
- 3.
- Run the same algorithm as the sender used for computing the
distribution
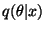 based on x.
based on x.
- 4.
- Decode the secondary message from
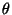 using
using
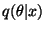 .
.
Again, the whole point in devising the coding scheme is not the actual
transmission of x, but learning about 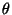 . In this case the
information about
. In this case the
information about 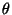 comes in the form of distribution
comes in the form of distribution
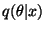 .
.
Computing all the terms, it turns out that
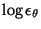 appears in both
appears in both 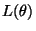 and
and
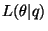 , but since these terms
appear with opposite signs,
, but since these terms
appear with opposite signs,
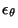 disappears from the
equations. The remaining terms are
disappears from the
equations. The remaining terms are
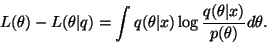 |
(20) |
This is the number of bits actually effectively used for encoding
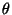 in the first part of the message. The length of the second
part of the message is
in the first part of the message. The length of the second
part of the message is
![\begin{displaymath}L(x \vert \theta) = - \int q(\theta \vert x) \log [p(x \vert \theta) \epsilon_x]
d\theta.
\end{displaymath}](img69.gif) |
(21) |
The total length of the message is thus
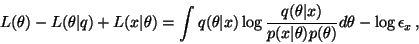 |
(22) |
which differs from the cost function (17) used in
ensemble learning only by the term
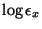 which can be
neglected as it does not depend on the approximation
which can be
neglected as it does not depend on the approximation
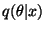 .
The bits-back argument thus results in ensemble learning.
.
The bits-back argument thus results in ensemble learning.
This derivation for ensemble learning is useful because it gives an
intuitive meaning for the cost function used in ensemble learning.
Different terms of the cost function can be interpreted as the number
of bits used for encoding various parameters and the observations. It
is then possible to see how many bits have been used for representing
different parameters and draw conclusions about the importance of the
parameter to the model.
At first glance, it might seem that minimum message length and
bits-back coding are quite different, the former using finite accuracy
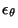 and the latter a very high accuracy
and the latter a very high accuracy
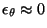 . It turns out, however, that the minimum message length
coding can be seen as a special case of bits-back coding where
. It turns out, however, that the minimum message length
coding can be seen as a special case of bits-back coding where
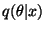 is chosen to be a uniform distribution between
is chosen to be a uniform distribution between
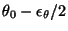 and
and
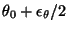 ,
where
,
where
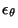 is the finite accuracy used in the minimum
message length scheme.
is the finite accuracy used in the minimum
message length scheme.



Next: Specification of the model
Up: Ensemble learning
Previous: Cost function
Harri Valpola
2000-10-31
![]() ,
the receiver should know the precision
,
the receiver should know the precision
![]() in addition
to the prior knowledge
in addition
to the prior knowledge ![]() , but
, but
![]() was not
included in the message. In [131], Wallace and Freeman
argued that the values and the accuracies of the parameters are not
independent, and one can construct a decodable message with almost the
same code length as in minimum message length coding.
was not
included in the message. In [131], Wallace and Freeman
argued that the values and the accuracies of the parameters are not
independent, and one can construct a decodable message with almost the
same code length as in minimum message length coding.
![]() [44]. The sender
uses the following coding scheme:
[44]. The sender
uses the following coding scheme:
![]() appears in both
appears in both ![]() and
and
![]() , but since these terms
appear with opposite signs,
, but since these terms
appear with opposite signs,
![]() disappears from the
equations. The remaining terms are
disappears from the
equations. The remaining terms are
![]() and the latter a very high accuracy
and the latter a very high accuracy
![]() . It turns out, however, that the minimum message length
coding can be seen as a special case of bits-back coding where
. It turns out, however, that the minimum message length
coding can be seen as a special case of bits-back coding where
![]() is chosen to be a uniform distribution between
is chosen to be a uniform distribution between
![]() and
and
![]() ,
where
,
where
![]() is the finite accuracy used in the minimum
message length scheme.
is the finite accuracy used in the minimum
message length scheme.