Publication IV discusses ensemble learning at
length, but this section describes briefly the cost function used in
ensemble learning. Let us denote the vector of all the unknown
variables of the model by
![]() and the vector of observations by
x and
suppose that the probabilities
and the vector of observations by
x and
suppose that the probabilities
![]() and
and
![]() are defined. According to Bayes' rule, the
posterior probability
are defined. According to Bayes' rule, the
posterior probability
![]() of the unknown variables is
of the unknown variables is
| (15) |
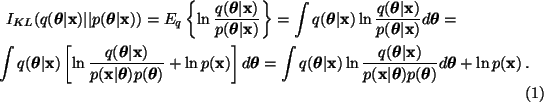
In order for ensemble learning to be computationally efficient, the
approximation
![]() should have a simple
factorial form. Then the cost function splits into a sum of simple
terms which can be computed efficiently.
should have a simple
factorial form. Then the cost function splits into a sum of simple
terms which can be computed efficiently.