Typically neural networks have relatively simple structure but many parameters, and it is usually easy to design a satisfactory coding for the structure. We shall therefore concentrate on measuring the description length of the parameters of the model.
If the transmitted data consists of discrete elements with known
probabilities, then the length needed in transmission can be computed.
It is well-known that if the probability of a data element D is
P(D), then the transmission of the element D using the optimal
code takes ![]() bits [9,8]. We shall
hereafter measure information in base e instead of base 2:
bits [9,8]. We shall
hereafter measure information in base e instead of base 2: ![]() bits equals
bits equals ![]() nats, where 1 nat equals
nats, where 1 nat equals ![]() bits.
bits.
The output data and the parameters in the network have continuous
values instead of discrete. Communicating a random continuous value
at an infinite precision would require an infinite number of bits, and
therefore the values have to be discretised. If the discretisation is
done with precision ![]() , then the range of values is divided
into small bins with size
, then the range of values is divided
into small bins with size ![]() . Suppose we know the
probability distribution p(x). If
. Suppose we know the
probability distribution p(x). If ![]() is small enough,
p(x) is approximately linear throughout each bin and the probability
of each bin is approximately
is small enough,
p(x) is approximately linear throughout each bin and the probability
of each bin is approximately ![]() , which means that the
description length L of the value x is
, which means that the
description length L of the value x is
| |
(1) |
The model is described by its structure, its parameters ![]() and their accuracies
and their accuracies
![]() . We shall consider a coding scheme where the
model is used to assign a probability distribution p(D) for each
data element
. We shall consider a coding scheme where the
model is used to assign a probability distribution p(D) for each
data element ![]() . Some of the parameters may also be
hyper parameters which are used to assign probability distribution
. Some of the parameters may also be
hyper parameters which are used to assign probability distribution
![]() for other parameters. The data is discretised with
accuracy
for other parameters. The data is discretised with
accuracy ![]() , but that can be considered an integral
part of the coding scheme. This is because the effect of
, but that can be considered an integral
part of the coding scheme. This is because the effect of
![]() does not depend on the model: it always adds a
constant
does not depend on the model: it always adds a
constant ![]() term in the description length,
and can therefore be omitted (N is the number of data elements). The
accuracy of the parameters (
term in the description length,
and can therefore be omitted (N is the number of data elements). The
accuracy of the parameters (![]() ) does depend on the
model, however, and must be taken into account.
) does depend on the
model, however, and must be taken into account.
In the literature, several different ways to measure the description length have been proposed. Our approach dates back to Wallace and Boulton [10] and similar approaches have been used in [4,11]. Alternative approaches have been presented e.g. in [6,7].
Suppose the target value for the parameter vector is ![]() . Let
us denote the actual discretised value by
. Let
us denote the actual discretised value by ![]() and the
corresponding round-off error by
and the
corresponding round-off error by ![]() . The errors depend on the locations of the borders between
the bins, but there is no reason to favour one discretisation over the
others, and therefore we should compute the expectation of the
description length over the distribution of
. The errors depend on the locations of the borders between
the bins, but there is no reason to favour one discretisation over the
others, and therefore we should compute the expectation of the
description length over the distribution of ![]() ,which is approximately even in the range
,which is approximately even in the range ![]() . We are also going to assume that the errors
are uncorrelated, that is,
. We are also going to assume that the errors
are uncorrelated, that is, ![]() .
.
The expected description length can be approximated by utilising the
second order Taylor's series expansion of ![]() about
about
![]() .
.
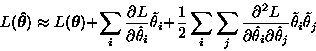 |
(2) |
| (3) |
Since the cost function includes second order derivatives of L with respect to the parameters, it might be troublesome to use it with a large neural network. First the outputs have to be computed in a feedforward phase as usual. Approximations of the second order derivatives needed in the cost function can be computed in a process analogous to backpropagation. It involves two feedback phases: the first one is used to compute the first order derivatives and the second one to compute the second order derivatives. It is then laborious to use backpropagation to compute the gradient, because it has to be applied to all three phases, resulting in a total of six phases.
Fortunately we can overcome these difficulties by recognising that it
is not the second order derivatives we wish to evaluate but the
expectation over ![]() .
.