 |
Intuitively, the idea behind MDL is that in order to be able to compress any given data one has to capture its regularities and structure. There are information-theoretical reasons why minimising the description length should yield models with good generalisation properties [5], and it has been shown in practise that description length has strong correlation with the expected classification error of an independent test set [3].
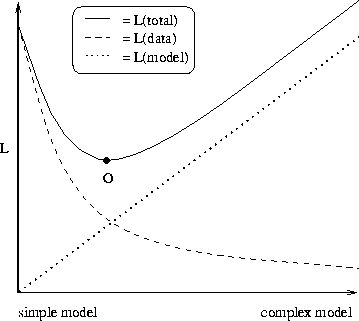
To understand the principle behind MDL, suppose there is a sender who wants to transmit a given data to a receiver. We shall assume that the sender will use a two-part coding scheme: he will first send a model of the data and then the data which is compressed using the model. The more bandwidth is used for the model the more the data is compressed. At some point, however, the cost of using a longer model becomes higher than the gain in compression of the data. Clearly, the length of the model should not exceed the length of the description of the data without using any model. Figure 1 shows schematically the relation between model complexity and the description length of the model and the data. Of course it is not necessary to actually code and transmit the model and the data in order to estimate the optimal model. It is enough to calculate what would be the description length if the data were compressed.
 |
The terms under- and over-fitting can be seen from MDL point of view. The optimal model is by our definition the one that has the minimum description length. Under-fitting means that the complexity of a model is below, and over-fitting that the complexity is above that of the optimal model.
It is important to recognise that the optimal model is not unique. Before transmitting the model and the data, the sender and the receiver must have agreed on how the message is coded, or otherwise the receiver would not know how to interpret it. The description length of the information used in the interpretation cannot be measured, because we would need to know how to interpret the coded interpretation, etc. Therefore there must always be some aspect of the model whose description length is neglected, namely the coding scheme. It determines the description length of the data, which means that models can only be compared with respect to a given coding scheme. Using Bayesian terms, the coding scheme implicitly defines a prior over the models. It is, however, often much easier to incorporate prior knowledge in the design of the code than assign a Bayesian prior over the models.