Inversion by Auxiliary MLP network

During learning, the sources have been co-adapted with the network. The mapping has first been fairly smooth and gradually evolved into a more nonlinear one. Since the model defines the mapping from sources to observations, it is not trivial to find the sources given the observations, that is, to invert the model. In many applications it is necessary to estimate the sources for new observations which have not been seen by the network during learning, however, and it can be asked whether the gradient based method is able to invert the network or will it get stuck in local minima.

**Figure 9:** Ten source signals estimated from the industrial pulp process. Time increases form left to right.
$\begin{figure}\epsfig{file=procsrc.eps,width=8.3cm} \end{figure}$

**Figure 10:** Each plot shown one of the thirty original time series on top of the nonlinear reconstruction made from the sources shown in Fig. 9.
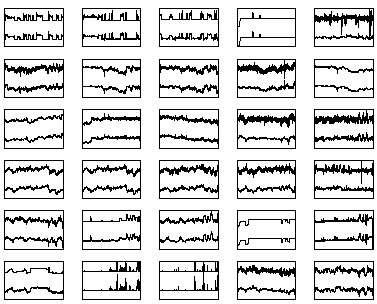$\begin{figure}\epsfig{file=procrec.eps,width=8.3cm} \end{figure}$

To test this, a new set of 1000 observation vectors were generated with the same generating MLP network as in the experiment with non-Gaussian artificial data in Sect. 3.3. Then several different techniques were tested for initialising the sources for the gradient descent based inversion of the same network whose results are shown in Fig. 8.

The best method turned out to be an auxiliary MLP network which was taught to approximate the inverse of the nonlinear mapping using Matlab Neural Network Toolbox. It had the same number of hidden neurons as the model MLP network and the numbers of inputs and output neurons had been switched to account for the inverse mapping. To teach the auxiliary MLP network we used the original data which was used in Sect. 3.3 and the sources estimated for that data. It is then possible to use the auxiliary MLP network to initialise the sources for new observations. A local minimum was detected only with four observations out of 1000.

**Figure 11:** Cost function as the number of sweeps.
$\begin{figure}\epsfig{file=auxmlp.eps,width=8.3cm} \end{figure}$

The naive initialisation with zeros is compared with the initialisation obtained by the auxiliary MLP network in Fig. 11. The case where all the sources have been set to the best values found is used as the baseline. On one hand, the figure shows that auxiliary MLP network gives a good initialisation, but on the other hand, it shows also that the auxiliary MLP network alone does not reach the quality obtained by gradient descent.