Non-Gaussian Sources

The following simulations demonstrate the capability of the algorithm to discover the underlying causes of the observations. The observations were generated by a randomly initialised MLP network as before. The generating MLP network had eight inputs, 30 hidden neurons and 20 outputs. Four of the sources were super-Gaussian and four were sub-Gaussian. Several MLP networks with different structures and initialisations were used for estimating the sources and the results obtained by the network which reached the lowest value of the cost function are presented here. This network had 50 hidden neurons.

**Figure 6:** Sources estimated by linear ICA.
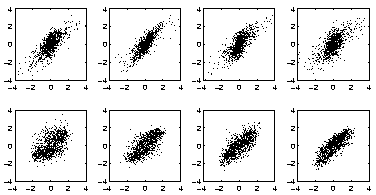
$\begin{figure}\epsfig{file=lin_ica1.eps,width=8.3cm} \end{figure}$

**Figure 7:** The nonlinear subspace has first been estimated by nonlinear FA (2000 sweeps). The the sources have been rotated by linear ICA.
$\begin{figure}\epsfig{file=nl_pca_ica.eps,width=8.3cm} \end{figure}$

**Figure 8:** The sources have further been refined by nonlinear IFA for another 5500 sweeps.
$\begin{figure}\epsfig{file=nl_ica.eps,width=8.3cm} \end{figure}$

FastICA, a well-known linear ICA algorithm, gives the sources shown in Fig. 6. On each of the eight scatter plots one of the original sources is plotted against the estimated source which best correlates with the original source. An optimal result would be a straight line on each plot. Judging from the plots in Fig. 6, linear ICA is not able to retrieve the original sources. This is also evident from the signal to noise ratio which is 0.7 dB. The inability of the linear ICA to find the original sources is caused by the mismatch between the actual generating model, which is nonlinear, and the assumed linear model.

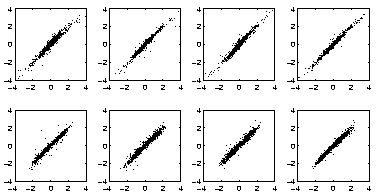
After 2000 sweeps with the nonlinear FA, that is, using only one Gaussian for modelling the distribution of each source, and a rotation with the FastICA, the sources have greatly improved as can be seen in Fig. 7. The nonlinear FA has been able to detect the nonlinear subspace in which the data points lie. The rotation ambiguity inherent in FA has been solved by the linear ICA. At this stage the signal to noise ratio is 13.2 dB.

Now the sources have non-Gaussian distributions and it is reasonable to use mixtures of Gaussians to model the distribution of each source. Three Gaussians were used for each mixture, but it would have been possible to optimise also the number of Gaussians. The results after another 5500 sweeps through the data are depicted in Fig. 8. The signal to noise ratio has further improved to 17.3 dB. Part of the improvement is due to fine-tuning of the nonlinear subspace which would have taken place even if only nonlinear FA were applied. However, the signal to noise ratio achieved by pure nonlinear FA applied for 7500 iterations is only 14.9 dB which shows that the network has also taken into account the non-Gaussian models of the sources.