

Next: Application to General ICA
Up: Fast Algorithms for Bayesian
Previous: Fast EM-algorithm by Filtering
The FastICA algorithm [5] can be interpreted as performing the above described
noise removal.
In FastICA the requirement of whitening the sources is also made and therefore
Rss=I and
(ATA)-1=I.
Then, the sources can be found one by one and we can consider a single column aof the mixing matrix A.
To derive the FastICA algorithm from the modified EM-algorithm, it is sufficient to note that
the term
XGF(s0G)T/M=as0GF(s0G)T/Mis
Cfa where Cf is a constant that depends only on the nonlinear function 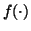 .
Then the update rule is
.
Then the update rule is
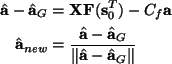
which is the FastICA algorithm, where the constant Cf is the expectation
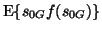 .
.
The choice of fixed nonlinearity 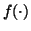 is implicitly connected to the distribution of the
sources s. The derivation of the EM-algorithm required that
is implicitly connected to the distribution of the
sources s. The derivation of the EM-algorithm required that
However, we see that 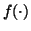 has certain degrees of freedom
due to taking the difference
XF(s0T)-XGF(s0GT).
Expanding f polynomially we obtain
has certain degrees of freedom
due to taking the difference
XF(s0T)-XGF(s0GT).
Expanding f polynomially we obtain
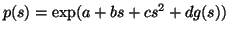 where
g'(s)=f(s) and g(s) contains
all the powers of f higher than two and possibly lower moments too.
This representation follows since in the update rule constants and
linear terms of
where
g'(s)=f(s) and g(s) contains
all the powers of f higher than two and possibly lower moments too.
This representation follows since in the update rule constants and
linear terms of 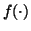 will cancel out. Therefore they will appear
in the distribution p(s) in the exponent with the power raised by
one due to integration. Since p(s) must be a probability density,
the constant a will be fixed by the requirement
will cancel out. Therefore they will appear
in the distribution p(s) in the exponent with the power raised by
one due to integration. Since p(s) must be a probability density,
the constant a will be fixed by the requirement
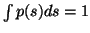 .
Mean and variance of s will determine the constants b and c,
since the sources are required to be zero-mean and whitened (variance
is fixed to unity). There is one free parameter d left, which means
that there is not only one distribution corresponding to
.
Mean and variance of s will determine the constants b and c,
since the sources are required to be zero-mean and whitened (variance
is fixed to unity). There is one free parameter d left, which means
that there is not only one distribution corresponding to 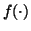 but a family of p(s). Typically the family includes both super- and
sub-Gaussian densities, which is why the same
but a family of p(s). Typically the family includes both super- and
sub-Gaussian densities, which is why the same 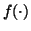 can be used
for both cases.
can be used
for both cases.


Next: Application to General ICA
Up: Fast Algorithms for Bayesian
Previous: Fast EM-algorithm by Filtering
Harri Lappalainen
2000-03-09
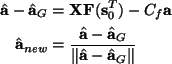
![]() .
Then the update rule is
.
Then the update rule is
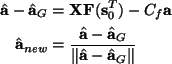
![]() .
.
![]() is implicitly connected to the distribution of the
sources s. The derivation of the EM-algorithm required that
is implicitly connected to the distribution of the
sources s. The derivation of the EM-algorithm required that