

Next: FastICA as EM-Algorithm with
Up: Fast Algorithms for Bayesian
Previous: EM-algorithm for Independent Component
With low noise variance 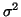 the convergence of the EM-algorithm
to the optimal value takes a time proportional to
the convergence of the EM-algorithm
to the optimal value takes a time proportional to
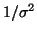 .
We
will next show how the re-estimation step can be modified so that the
convergence rate will be independent of
.
We
will next show how the re-estimation step can be modified so that the
convergence rate will be independent of 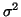 which yields a
significant speedup if
which yields a
significant speedup if 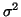 is small.
is small.
Consider the case that we estimate the sources one at a time and that
the sources are assumed to be whitened and the mixing matrix
A orthonormal. Denote one of the source signals in the optimal
solution as
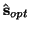 .
By optimality we mean that the
standard EM-algorithm will eventually converge to
.
By optimality we mean that the
standard EM-algorithm will eventually converge to
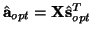 with
with
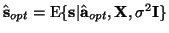 .
.
When we have not yet found the optimal vector
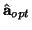 ,
we have
,
we have
where
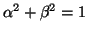 .
The noise
sG is mostly due to
the other sources and to a small extent the Gaussian noise in the
data. We can think that the E-step filters away the noise by making
use of the knowledge about the prior distribution of s.
This gives one point of view into the slow convergence: in low noise
case most of the unwanted signal
sG is due to other sources
and a slow convergence results. From this point of view, it is
obvious that we can speed up the convergence if we can filter away
also that part of
sG which is due to other sources.
.
The noise
sG is mostly due to
the other sources and to a small extent the Gaussian noise in the
data. We can think that the E-step filters away the noise by making
use of the knowledge about the prior distribution of s.
This gives one point of view into the slow convergence: in low noise
case most of the unwanted signal
sG is due to other sources
and a slow convergence results. From this point of view, it is
obvious that we can speed up the convergence if we can filter away
also that part of
sG which is due to other sources.
When we are far from the optimal solution, it is natural to
assume that
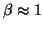 and
and
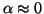 .
Since aand
s0 are linearly related, we get
.
Since aand
s0 are linearly related, we get
If we can compute
aG, we can adjust the vector ato take into account the apparent noise due to other sources. By the
central limit theorem, the distribution of the sum of contributions
from several other sources approaches Gaussian as the number of other
sources increases. This leads to the following modification: we may
estimate
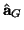 using the same re-estimation whose result
will be approximately
using the same re-estimation whose result
will be approximately
where
XG is the set of mixtures replaced by Gaussian noise
with the same covariance as X and
s0G is the
source obtained as
aTXG. The Gaussian source
s0G is the projection of Gaussian noise to the subspace
spanned by a and therefore represents the contribution of
the other sources and some Gaussian noise to the estimated source
s0. As derived above, we can eliminate much of this noise
by updating a using the difference
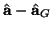 which is then normalized. The normalization can be done,
since scaling of the sources is an undeterminacy in ICA.
which is then normalized. The normalization can be done,
since scaling of the sources is an undeterminacy in ICA.
Taking the difference yields approximately
which shows that the normalization cancels the effect of 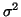 from the learning rule:
from the learning rule:
We assumed above that there was a lot of Gaussian noise by
approximating
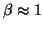 .
It turns out that the above
modification does not affect the optimal solutions of the algorithm,
i.e., if
.
It turns out that the above
modification does not affect the optimal solutions of the algorithm,
i.e., if
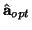 is a fixed point of the original
EM-algorithm, it is also a fixed point of the modified algorithm.
This follows immediately from the fact that
is a fixed point of the original
EM-algorithm, it is also a fixed point of the modified algorithm.
This follows immediately from the fact that
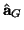 is
always parallel to a since
XG is spherically symmetric.
To get a rough idea about why this is so, suppose there is a vector
b which is orthogonal to a, i.e.,
bT
a = 0. Then
is
always parallel to a since
XG is spherically symmetric.
To get a rough idea about why this is so, suppose there is a vector
b which is orthogonal to a, i.e.,
bT
a = 0. Then
The last step follows from the fact that
s0G' is a
projection to an orthogonal direction form
s0G and by
Gaussianity of
XG, statistically independent form
F(s0G). But since this must hold for all b which are
orthogonal to a, it follows that
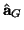 has to
be parallel to a.
has to
be parallel to a.
In the next section we add validity to the result by showing that
FastICA algorithm follows from this procedure.


Next: FastICA as EM-Algorithm with
Up: Fast Algorithms for Bayesian
Previous: EM-algorithm for Independent Component
Harri Lappalainen
2000-03-09
![]() the convergence of the EM-algorithm
to the optimal value takes a time proportional to
the convergence of the EM-algorithm
to the optimal value takes a time proportional to
![]() .
We
will next show how the re-estimation step can be modified so that the
convergence rate will be independent of
.
We
will next show how the re-estimation step can be modified so that the
convergence rate will be independent of ![]() which yields a
significant speedup if
which yields a
significant speedup if ![]() is small.
is small.
![]() .
By optimality we mean that the
standard EM-algorithm will eventually converge to
.
By optimality we mean that the
standard EM-algorithm will eventually converge to
![]() with
with
![]() .
.
![]() ,
we have
,
we have
![]() and
and
![]() .
Since aand
s0 are linearly related, we get
.
Since aand
s0 are linearly related, we get
![]() .
It turns out that the above
modification does not affect the optimal solutions of the algorithm,
i.e., if
.
It turns out that the above
modification does not affect the optimal solutions of the algorithm,
i.e., if
![]() is a fixed point of the original
EM-algorithm, it is also a fixed point of the modified algorithm.
This follows immediately from the fact that
is a fixed point of the original
EM-algorithm, it is also a fixed point of the modified algorithm.
This follows immediately from the fact that
![]() is
always parallel to a since
XG is spherically symmetric.
To get a rough idea about why this is so, suppose there is a vector
b which is orthogonal to a, i.e.,
bT
a = 0. Then
is
always parallel to a since
XG is spherically symmetric.
To get a rough idea about why this is so, suppose there is a vector
b which is orthogonal to a, i.e.,
bT
a = 0. Then