EM-algorithm for Independent Component Analysis

In the signal model only the vectors x(t) are observed. Everything else is unknown and must be estimated using the data. In general, the task is to compute the joint posterior distribution for all the unknown parameters conditioned by the mixtures x(t).

A more simple case is when the maximum likelihood estimate is used for some on the parameters. This can be done by the EM-algorithm where the computation alternates between computing the posterior distribution of one set of variables given the current point estimate of the other set of variables (E-step) and then using the posterior distribution of the first set of variables to compute a new maximum likelihood estimate of the second set of variables (M-step).

When EM-algorithm is applied to ICA, usually the full posterior distribution is computed for sources and the maximum likelihood estimate is used for the rest of the parameters. This means that in the E-step we need to compute the posterior distribution of the sources s given x,A and the noise covariance $\sigma^2\mathbf I$

$$p(\mathbf s\vert\mathbf A,\mathbf x,\sigma^2\mathbf I)$$

and use it to update our estimates.

Using the matrix notation for the finite number of samples, i.e. X and S, we can write the M-step (see [9]) re-estimation for the mixing matrix as

$$\hat\mathbf A=\mathbf R_{xs}\mathbf R_{ss}^{-1}$$

where the posterior correlation matrices are
$$\begin{align*}\mathbf R_{xs}&=\frac 1M\sum_i \mathbf x(i)\operatorname{E}\{\math... ...x(i),\mathbf A,\sigma^2\mathbf I\}=\mathbf{ \widehat{S S}}^T/M \, . \end{align*}$$
The expectations are taken over the posterior distribution of the sources.

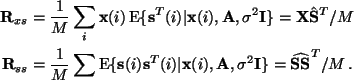
We will consider here the case where $\sigma^2$ is small. If we further assume that the mixtures are prewhitened, we can constrain the mixing matrix to be orthogonal and we can assume that the sources have unit variance. This makes R_ss a unit matrix.

In [2] the EM-algorithm is derived as a low-noise approximation for the case of square mixing matrix A. First, the posterior mean $p(\mathbf s\vert\mathbf A,\mathbf x,\sigma^2\mathbf I)$ is obtained as

$$\hat \mathbf s=\operatorname{E}\{\mathbf s\vert\mathbf A,\mat... ...\mathbf s_0 +\sigma^2(\mathbf A^T\mathbf A)^{-1}f(\mathbf s_0)$$

where $f(\cdot)$ is the derivative $\frac{\partial \log p_i(s_i)}{\partial s_i}$and s₀=A^-1x. Since we assumed that the mixing matrix is orthogonal, we can omit the term (A^TA)^-1 and we get

$$\hat \mathbf s=\operatorname{E}\{\mathbf s\vert\mathbf A,\mat... ...,\sigma^2\mathbf I\}\approx\mathbf s_0 +\sigma^2f(\mathbf s_0)$$

Substituting the above approximations we get
$$\begin{align*}\hat\mathbf A&=\mathbf X\hat\mathbf S^T/M\\ &\approx\mathbf X\mat... ...S_0^T)/M\\ &=\mathbf A+\sigma^2\mathbf X\mathbf F(\mathbf S_0^T)/M \end{align*}$$

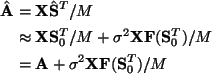
As the authors mention in [2], this approximation leads to an EM-algorithm which converges slowly with low noise variance $\sigma^2$. They also point out that there is no visible ``noise-correction''. It is precisely this point that we will address in the next section.