An important aspect of any kind of information processing is the way in which the information is represented. In the brain it could be represented by the activity of single, individually meaningful neurons, or it could be that only the global activity pattern across a whole neuron population corresponds to interpretable states. There are strong theoretical reasons and experimental evidence [Földiák and Young, 1995, Thorpe, 1995] suggesting that the brain adopts a compromise between these extremes which is often referred to as sparse coding.
Let us suppose that there are binary coding units, neurons, which can be either ``active'' or ``passive''. An important characteristic of such a code is the activity ratio, the fraction of active neurons at any one time. At its lowest value it is local representation, where each state is represented by a single active unit from a pool in which all other units are silent, somewhat like the letters on a typewriter keyboard that are locally encoded. In dense distributed representation, each state is represented on average by about half of the units being active. Examples of this are the binary (ASCII) encoding of characters used in computers or the coding of visual images by the retinal photoreceptor array. Codes with low activity ratios are called sparse codes.
When the neurons have graded outputs it is more difficult to give a
simple measure of sparseness. One is the entropy of the
outputs[Attneave, 1954, Barlow, 1960, Watanabe, 1981], which decreases as the
outputs become sparser. It is difficult to measure the entropy
directly, but in some cases the kurtosis
of the outputs can be used instead
[Field, 1994]. The sparser the outputs, the larger the kurtosis.
Although sparse codes do have large kurtosis, the opposite does not
necessarily hold. It is possible to construct dense codes with large
kurtosis [Baddeley, 1996]. In this work, a somewhat heuristic
definition of sparseness for graded outputs is used. The code is said
to be sparse if a small fraction of the inputs convey most of the
information.
The activity ratio affects several aspects of information processing such as the architecture and robustness of networks, the number of distinct states that can be represented and stored, generalisation properties, and the speed and rules of learning (Table 1.1).
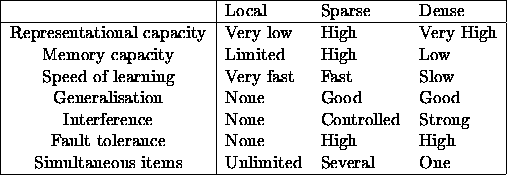
Table:
Properties of coding schemes according to Földiák and Young (1995).
The representational capacity of local codes is small: they can
represent only as many states as the number of units in the pool,
which is insufficient for any but the most trivial tasks. Even when
the number of units is as high as that in primate
cortex, the number of discriminable states
well exceeds this number. Making associations between a locally
encoded item and an output, however, is easy and fast. Single-layer
networks can learn any output association in a single trial by local,
Hebbian strengthening of connections between active representation and
output units, and the linear separability problem does not arise. In
such a lookup table, there is no interference between
associations to other discriminable states, and learning information
about new states does not interfere with old associations. This,
however, also means that there will be no generalisation to other
discriminable states -- which is a fundamental flaw, as we can expect
a system never to experience precisely the same pattern of stimulation
twice.
Dense distributed codes, on the other hand, can represent a very high
number (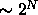 
, where N is the number of units) of different
states by combinatorial use of units. They are best suited for
minimising the number of neurons needed to represent information. If
the number of available neurons is high enough, the representational
power is largely superfluous, as the number of patterns ever
experienced by the system will never approach the available capacity,
and therefore dense codes usually have high statistical redundancy.
The price to pay for the potential (but unused) high information
content of each pattern is that the number of such patterns that an
associative memory can store is unnecessarily low. The mapping
between a dense representation and an output can be complex (a
linearly nonseparable function), therefore requiring multilayer
networks and learning algorithms that are hard to implement
biologically. Even efficient supervised algorithms are prohibitively
slow, requiring many training trials and large amounts of the kind of
training data that is labelled with either an appropriate output or
reinforcement. Such data is often too risky, time consuming, or
expensive to obtain. Distributed representations in intermediate
layers of such networks ensure a kind of automatic generalisation
[Hinton et al., 1986]. However, this often manifests itself as unwanted
interference between patterns. A further serious problem is that no
new associations can be added without retraining the network with the
complete training set.
Sparse codes combine advantages of local and dense codes while avoiding most of their drawbacks. Codes with small activity ratios can still have sufficiently high representational capacity, while the number of input-output pairs that can be stored in an associative memory is far greater for sparse than for dense patterns [Meunier and Nadal, 1995]. This is achieved by decreasing the amount of information in the representation of any individual stored pattern. As a much larger fraction of all input-output functions are linearly separable using sparse coding, a single supervised layer with simple learning rules, following perhaps several unsupervised layers, is more likely to be sufficient for learning target outputs, avoiding problems associated with supervised training in multilayer networks. As generalisation takes place only between overlapping patterns, new associations will not interfere with previous associations to nonoverlapping patterns.
Sparseness can also be defined with respect to components. A scene may be encoded in a distributed representation while, at the same time, object features may be represented locally. The number of simultaneously presented items decreases as activity ratio increases because the addition of active units eventually results in activation of ``ghost'' subsets, corresponding to items that were not intended to be activated.