The neurons compute the projection in the direction of their weight vectors. Therefore the output of a neuron before the winning strength assignment is the cosine of the angle between the input and the weight vector multiplied with the norm of the input vector. The outputs are limited to be positive, and so the output of a single neuron looks like a cut sinusoidal after the winning strength assignment. When there are more than one neuron, they compete for the input. Generally it can be said that neurons compete the stronger with each other the closer their weight vectors are. If there are two sets of neurons which have orthogonal weight vectors, their winning strengths are independent, and therefore the system can convey independent information in parallel.
Figure 4.3 shows the shape of y, when the input is
2-dimensional, and there are three evenly spaced weight vectors. A
notable property of 
is that they depend only on the direction of
the input, not the amplitude. Therefore the y are linearly
dependent on the length of the input. The length of input vector has
been normalised to unity, but the shape of the outputs would remain
unchanged also for different lengths of input. In this test, the
parameter 
, which governs the amount of inhibition, has been
one. When the weight vectors are orthogonal there is no competition,
and the neurons work completely independently. When the weight
vectors become more parallel the amount of competition increases,
which sharpens the outputs.
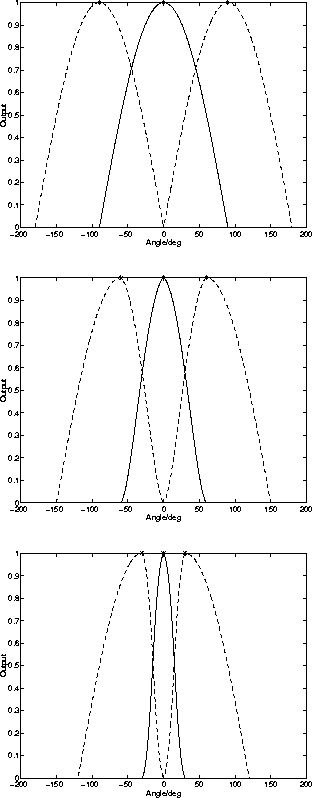
Figure 4.3:
The response for the middle neuron becomes more sharply tuned due
to competition when the adjacent neurons come close. X-axis shows
the angle between the input and the middle neuron. Places of
weight vectors are denoted by `*'. At the top, the angles
between neurons are 
and there is no competition. In
the middle, the angles are 
and at the bottom
. Parameter 
.
Figure 4.4 shows the effect of parameter . The
larger the the stronger the inhibition. When
approaches infinity, the winning strengths become binary. From the
figure it can be seen that increasing makes the transition
between winners sharper.
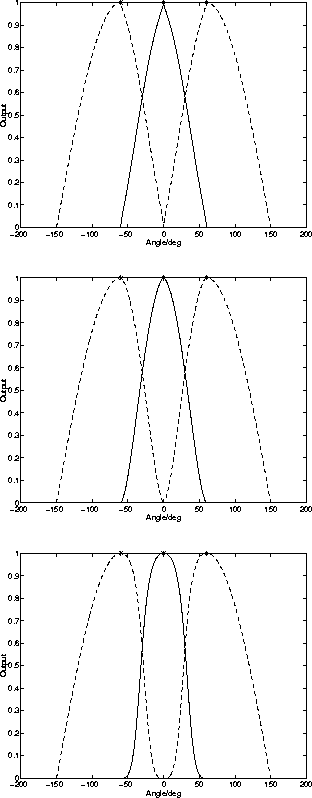
Figure 4.4:
The transition between winners becomes sharper as the parameter
which governs the amount of inhibition increases. At the
top 
, at the middle , and at the bottom
. The angle between the neurons was .
Figure 4.5 shows the shape of y when the input space is
3-dimensional. Weight vectors are nearly parallel and are organised
on a 2-dimensional lattice. The figure shows that the properties
demonstrated in two dimensions generalise in higher dimensions.
The figure shows again how increasing makes the transition
between winners sharper.
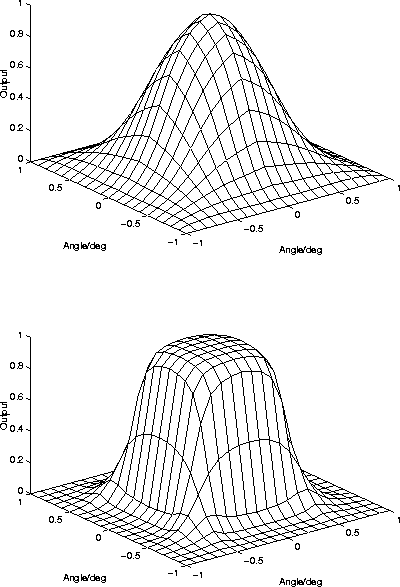
Figure 4.5:
Nine nearly parallel weight vectors are organised on a
2-dimensional lattice (angles 
, 
and 
in both x- and y-axis). The plots show the y of the neuron in
the middle. At the top, parameter . At the bottom
.
Figure 4.6 shows what happens when there are orthogonal sets of nearly parallel weight vectors. The competition occurs only inside one set and therefore the system has several independent parts, which enables the system to process information in parallel. The competition inside the sets makes the responses sharply tuned and results in a sparse code.
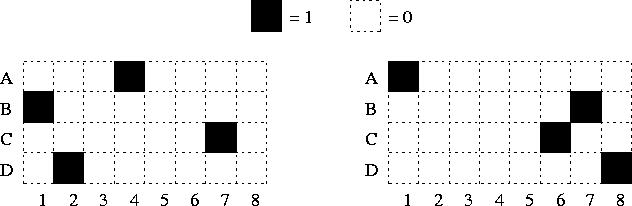
Figure:
Outputs of a network with 32 neurons. There are four sets (A, B,
C and D) of eight (1-8) nearly parallel weight vectors. The
weight vectors between two different sets are orthogonal, and thus
there are four independently functioning parts in the network.
The inputs were superpositions of four orthogonal vectors, one
weight vector from each set. The outputs show that there is no
cross-talk between orthogonal sets. Inside one set the neurons
compete with each other, and since the input is a sum of weight
vectors the outputs are binary. (If the input had fell between
two weight vectors they would have had graded outputs as in
figures 4.3-4.5.)