In ensemble learning, the goal is to approximate the posterior pdf of
all the unknown values in the model. Let us denote the observations
by
X. Everything else in the model is unknown, i.e., the
sources, parameters and hyperparameters. Let us denote all these
unknowns by the vector
![]() .
The cost function measures the
misfit between the actual posterior pdf
.
The cost function measures the
misfit between the actual posterior pdf
![]() and its approximation
and its approximation
![]() .
.
The posterior is approximated as a product of independent Gaussian
distributions
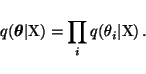 |
(16) |
The functional form of the cost function
![]() is given in Chap. 6.
The cost function can be interpreted to measure the misfit between the
actual posterior
is given in Chap. 6.
The cost function can be interpreted to measure the misfit between the
actual posterior
![]() and its factorial
approximation
and its factorial
approximation
![]() .
It can also be
interpreted as measuring the number of bits it would take to encode
X when approximating the posterior pdf of the unknown
variables by
.
It can also be
interpreted as measuring the number of bits it would take to encode
X when approximating the posterior pdf of the unknown
variables by
![]() .
.
The cost function is minimised with respect to the posterior means
![]() and variances
and variances
![]() of the unknown
variables
of the unknown
variables ![]() .
The end result of the learning is therefore not
just an estimate of the unknown variables, but a distribution over the
variables.
.
The end result of the learning is therefore not
just an estimate of the unknown variables, but a distribution over the
variables.
The simple factorising form of the approximation
![]() makes the cost function computationally tractable. The
cost function can be split into two terms, Cq and Cp, where the
former is an expectation over
makes the cost function computationally tractable. The
cost function can be split into two terms, Cq and Cp, where the
former is an expectation over
![]() and the
latter is an expectation over
and the
latter is an expectation over
![]() .
.
It turns out that the term Cq is not a function of the posterior
means
![]() of the parameters, only the posterior
variances. It has a similar term for each unknown variable.
of the parameters, only the posterior
variances. It has a similar term for each unknown variable.
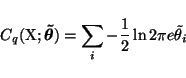 |
(17) |
Most of the terms of Cp are also trivial. The Gaussian densities
in (8)-(15) yield terms of the form
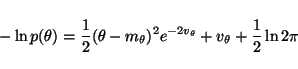 |
(18) |
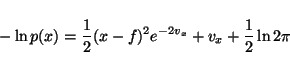 |
(20) |
The function f consists of two multiplications with matrices and a
nonlinearity in between. The posterior mean and variance for a
product u = yz are
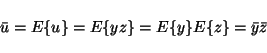 |
(22) |
Let us now pick one hidden neuron having nonlinearity g and input
![]() ,
i.e., the hidden neuron is computing
,
i.e., the hidden neuron is computing ![]() .
At this point
we are not assuming any particular form of g although we are going
to use
.
At this point
we are not assuming any particular form of g although we are going
to use
![]() in all the experiments; the following
derivation is general and can be applied to any sufficiently smooth
function g.
in all the experiments; the following
derivation is general and can be applied to any sufficiently smooth
function g.
In order to be able to compute the posterior mean and variance of the
function g, we are going to apply the Taylor's series expansion
around the posterior mean ![]() of the input. We choose the
second order expansion when computing the mean and the first order
expansion when computing the variance. The choice is purely
practical; higher order expansions could be used as well but these are
the ones that can be computed from the posterior mean and variance of
the inputs alone.
of the input. We choose the
second order expansion when computing the mean and the first order
expansion when computing the variance. The choice is purely
practical; higher order expansions could be used as well but these are
the ones that can be computed from the posterior mean and variance of
the inputs alone.
![\includegraphics[width=2.5cm]{paths.eps}](img65.gif) |
The reason for the outputs of the hidden neurons to be posteriorly
dependent is that the value of one source can potentially affect all
the outputs. This is illustrated in Fig. 4. Each
source affects the output of the whole network through several paths
and in order to be able to determine the variance of the outputs, the
paths originating from different sources need to be kept separate.
This is done by keeping track of the partial derivatives
![]() .
Equation (26)
shows how the total posterior variance of the output
.
Equation (26)
shows how the total posterior variance of the output ![]() of one
of the hidden neurons can be split into terms originating from each
source plus a term
of one
of the hidden neurons can be split into terms originating from each
source plus a term
![]() which contains the variance
originating from the weights and biases, i.e., those variables which
affect any one output through only a single path.
which contains the variance
originating from the weights and biases, i.e., those variables which
affect any one output through only a single path.
The only approximations done in the computation are the ones approximating the effect of nonlinearity. If the hidden neurons were linear, the computation would be exact. The nonlinearity of the hidden neurons is delt with by linearising around the posterior mean of the inputs of the hidden neurons. The smaller the variances the more accurate this approximation is. With increasing nonlinearity and variance of the inputs, the approximation gets worse.
Compared to ordinary forward phase of an MLP network, the computational complexity is greater by about a factor of 5N, where N is the number of sources. The factor five is due to propagating distributions instead of plain values. The need to keep the paths originating from different sources separate explains the factor N. Fortunately, much of the extra computation can be made into good use later on when adapting the distributions of variables.