
Next: Cost Function
Up: Nonlinear Factor Analysis
Previous: Nonlinear Factor Analysis
Figure 3:
The mapping from sources to observations is modelled by the
familiar MLP network. The sources are on the top layer and
observations in the bottom layer. The middle layer consists of
hidden neurons each of which computes a nonlinear function of the
inputs
|
|
The schematic structure of the mapping is shown in Fig. 3.
The nonlinearity of each hidden neuron is the hyperbolic tangent,
which is the same as the usual logistic sigmoid except for a scaling.
The equation defining the mapping is
 |
(3) |
The matrices A and B are the weights of first and second layer and
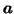 and
and 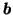 are the corresponding biases.
are the corresponding biases.
The noise is assumed to be independent and Gaussian and therefore the
probability distribution of x(t) is
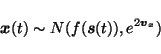 |
(4) |
Each component of the vector 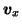 gives the log-std of the
corresponding component of
gives the log-std of the
corresponding component of
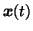 .
.
The sources are assumed to have zero mean Gaussian distributions and
again the variances are parametrised by log-std 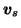 .
.
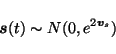 |
(5) |
Since the variance of the sources can vary, variance of the weights
A on the first layer can be fixed to a constant, which we
choose to be one, without loosing any generality from the model. This
is not case for the second layer weights. Due to the nonlinearity,
the variances of the outputs of the hidden neurons are bounded from
above and therefore the variance of the second layer weights cannot be
fixed. In order to enable the network to shut off extra hidden
neurons, the weights leaving one hidden neuron share the same variance
parameter![[*]](foot_motif.gif) .
.
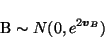 |
(6) |
The elements of the matrix
B are assumed to have a zero mean
Gaussian distribution with individual variances for each column and
thus the dimension of the vector 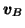 is the number of hidden
neurons. Both biases
is the number of hidden
neurons. Both biases 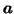 and
and 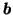 have Gaussian
distributions parametrised by mean and log-std.
have Gaussian
distributions parametrised by mean and log-std.
The distributions are summarised in
(7)-(12).
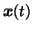 |
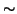 |
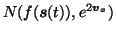 |
(7) |
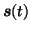 |
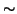 |
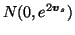 |
(8) |
| A |
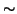 |
N(0, 1) |
(9) |
| B |
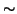 |
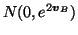 |
(10) |
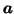 |
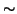 |
N(ma, e2va) |
(11) |
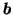 |
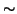 |
N(mb, e2vb) |
(12) |
The distributions of each set of log-std parameters are modelled by
Gaussian distributions whose parameters are usually called
hyperparameters.
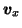 |
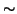 |
N(mvx, e2vvx) |
(13) |
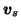 |
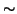 |
N(mvs, e2vvs) |
(14) |
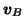 |
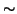 |
N(mvB, e2vvB) |
(15) |
The prior distributions of ma, va, mb, vb and the six
hyperparameters
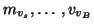 are assumed to be Gaussian
with zero mean and standard deviation 100, i.e., the priors are
assumed to be very flat.
are assumed to be Gaussian
with zero mean and standard deviation 100, i.e., the priors are
assumed to be very flat.


Next: Cost Function
Up: Nonlinear Factor Analysis
Previous: Nonlinear Factor Analysis
Harri Lappalainen
2000-03-03
![\includegraphics[width=8cm]{mlp.eps}](img11.gif)
![\includegraphics[width=8cm]{mlp.eps}](img11.gif)

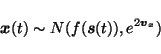
![]() .
.
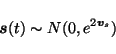
![[*]](foot_motif.gif) .
.