Instead of assuming the form for the approximate posterior distribution we could instead derive the optimal separable distribution (the functions that minimise the cost function subject to the constraint that they be normalised).
Instead of learning the log-std
![]() ,
we shall learn the inverse noise variance
,
we shall learn the inverse noise variance
![]() .
The prior on
.
The prior on ![]() is assumed to be a Gamma distribution of the form
is assumed to be a Gamma distribution of the form
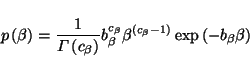 |
(34) |
The cost function that must be minimised is now
| C | = | ||
| = | 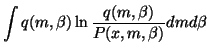 |
(35) |
| C | = | ![$\displaystyle \int q(m)q(\beta)\ln \frac{q(m)q(\beta)}{\left[ \prod_t P(x(t) \vert m, \beta) \right] P(m) P(\beta)} dm d\beta$](img140.gif) |
|
| = | 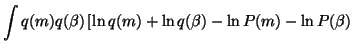 |
||
![$\displaystyle \left. -\sum_t \left( \frac{1}{2}\ln \frac{\beta}{2 \pi} -\frac{\beta \left(x(t)-m\right)^2}{2} \right)\right] dm d\beta$](img142.gif) |
(36) |
![\begin{displaymath}C= \int q(m)\left[\ln q(m) - \ln P(m) -\sum_t \left( -\frac{\bar{\beta} \left(x(t)-m\right)^2}{2} \right) \right] dm
\end{displaymath}](img144.gif) |
(37) |
 |
= | 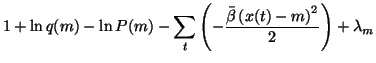 |
|
| = | 0 | (38) |
| = | 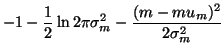 |
||
| = | 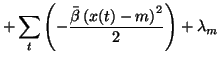 |
(39) |
We can obtain the optimum form for ![]() by marginalising the cost function over m and dropping terms independent of
by marginalising the cost function over m and dropping terms independent of ![]() .
.
| C | = | 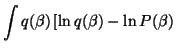 |
|
![$\displaystyle \left.-\sum_t \left( \frac{1}{2}\ln \beta -\frac{\beta \left(\left(x(t)-\bar{m}\right)^2+ \tilde{m}\right)}{2} \right) \right] d\beta$](img155.gif) |
(40) |
| = | |||
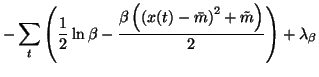 |
|||
| = | 0 | (41) |
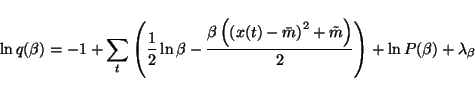 |
(42) |
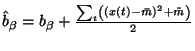 and
and
The optimal distributions for m and ![]() depend on each other (q(m) is a function of
depend on each other (q(m) is a function of
![]() and
and ![]() is a function of
is a function of ![]() and
and ![]() )
so the optimal solutions can be found by iteratively updating q(m) and
)
so the optimal solutions can be found by iteratively updating q(m) and ![]() .
.
A general point is that the freeform optimisation of the cost function will typically lead to a set of iterative update equations where each distribution is updated on the basis of the other distributions in the approximation.
We can also see that if the parametrisation of the model is chosen appropriately the optimal separable model has a similar form to the prior model. If the prior distributions are Gaussians the posterior distributions are also Gaussians (likewise for Gamma distributions). If this is the case then we can say that we have chosen conjugate priors.
![\includegraphics[width=10.0cm]{prob_contour2.eps}](img163.gif) |
Figure 4 shows a comparison of the true posterior distribution and the approximate posterior. The data set is the same as for the fixed form example. The contours in both distributions are centred in the same region, a model that underestimates m. The contours for the two distributions are qualitatively similar, the approximate distribution also shows the assymmetric density.