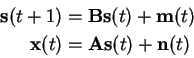 |
(4.12) |
The linear state-space model (SSM) is built from a standard linear dynamical system in Equation (2.4). However, the state is not observed directly but only through another linear mapping. The basic model can be described by a pair of equations:
As we saw in Section 2.1.2, the possible dynamics of such a linear model are very restricted. The process noise may help in keeping the whole system from converging to a single point, but still the system cannot explain any interesting complex phenomena.
Linear SSMs are nevertheless used widely because they are very efficient to use and provide a good enough short-term approximation for many cases even if the true dynamics are nonlinear.
The most famous variant of linear SSMs is the Kalman filter [31,41,32]. It gives a learning algorithm for the model defined by Equation (4.12) assuming all the parameters are Gaussian and certain independence assumptions are met. Kalman filtering is used in several application because it is easy to implement and efficient.