


Next: Nonlinear systems and chaos
Up: Theory
Previous: Dynamical systems
Contents
Linear systems
Let us assume that the mapping
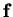 in
Equation (2.1) is linear, i.e.
in
Equation (2.1) is linear, i.e.
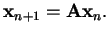 |
(2.4) |
Iterating the system for a given initial vector
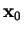 leads to a
sequence
leads to a
sequence
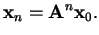 |
(2.5) |
The possible courses of evolution of such sequences can be
characterized by the eigenvalues of the matrix
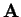 . If there are
eigenvalues that are greater than one in absolute value, almost all of
the orbits will diverge to infinity. If all the eigenvalues are less
than one in absolute value, the orbits will rapidly converge to the
origin. Complex eigenvalues with absolute value of unity will lead to
closed circular or elliptic orbits [1].
. If there are
eigenvalues that are greater than one in absolute value, almost all of
the orbits will diverge to infinity. If all the eigenvalues are less
than one in absolute value, the orbits will rapidly converge to the
origin. Complex eigenvalues with absolute value of unity will lead to
closed circular or elliptic orbits [1].
An affine map with
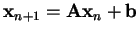 behaves in
essentially the same way. This shows that the autonomous linear
system is too simple to describe any interesting dynamical phenomena,
because in practice the only stable linear systems converge
exponentially to a constant value.
behaves in
essentially the same way. This shows that the autonomous linear
system is too simple to describe any interesting dynamical phenomena,
because in practice the only stable linear systems converge
exponentially to a constant value.



Next: Nonlinear systems and chaos
Up: Theory
Previous: Dynamical systems
Contents
Antti Honkela
2001-05-30
![]() in
Equation (2.1) is linear, i.e.
in
Equation (2.1) is linear, i.e.
![]() behaves in
essentially the same way. This shows that the autonomous linear
system is too simple to describe any interesting dynamical phenomena,
because in practice the only stable linear systems converge
exponentially to a constant value.
behaves in
essentially the same way. This shows that the autonomous linear
system is too simple to describe any interesting dynamical phenomena,
because in practice the only stable linear systems converge
exponentially to a constant value.